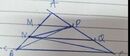
Trong hình bên, ABC là một tam giác có diện tích 2020 cm2. M và N nằm trên AB sao cho AM = MN = NB/2 . P và Q nằm trên AC sao cho CP = PQ = QA/2 . Tính diện tích của hình tứ giác MQPN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bn làm kiểu gì mà ra 670 cm2 vậy tíntiếnngân ( bạn có thể giải thích được ko)

A M N B C P Q
1. nối nc và mc, ta có acn = ncm = mcb ( vì chung chiều cao hạ từ đỉnh c và có độ dài đáy bằng nhau )
=> acn = ncm = mcb = 2010 : 3 = 670 ( cm2 )
2. nối mq, từ 1, ta có apm = pqm = qcm = 670/ 3 ( cm2 )
3.từ 1 và 2, ta có mqo = qco = 670/3 : 2 = 335/ 3 ( cm2 ) [mình quên chưa đánh dấu điểm x, điểm x là điểm giao nhau của cm và qn]
4. từ 1,2,3, ta có cmx = xmn = 670 : 2 = 335 ( cm2 )
vậy diện tích của mnpq là
335+335/3+670/3 = 670( cm2 )
đáp số670( cm2 )

Diện tích tam giác ABP bằng 2010÷ 3( vì cùng chiều cao xuata phát từ B với tam giác ABC và đáy AP bằng 1/3 AC). Diện tích tg PMN bằng 1/3 dt tg ABP = 670/3( vì chung đcao xphat từ P và đáy bằng 1/ 3 đáy AB). Dt tg ANC bằng 2/3 dt tg ABC = 1340, dttg NPQ bằng 1/3 dttg ANC = 1340/3. DtMNQP = dttg PMN + NPQ = 670

\(AM=MN=\frac{NB}{2}\Rightarrow AM=\frac{1}{4}\times AB,AN=\frac{1}{2}\times AB\)
\(CP=PQ=\frac{QA}{2}\Rightarrow AQ=\frac{1}{2}\times AC,AP=\frac{3}{4}\times AC\)
\(S_{AMC}=\frac{1}{4}\times S_{ABC}\)(chung đường cao hạ từ \(C\), \(AM=\frac{1}{4}\times AB\))
\(S_{AMQ}=\frac{1}{2}\times S_{AMC}\)(chung đường cao hạ từ \(M\), \(AQ=\frac{1}{2}\times AC\))
Suy ra \(S_{AMQ}=\frac{1}{2}\times\frac{1}{4}\times S_{ABC}=\frac{1}{8}\times S_{ABC}\)
\(S_{ANC}=\frac{1}{2}\times S_{ABC}\)(chung đường cao hạ từ \(C\), \(AN=\frac{1}{2}\times AB\))
\(S_{ANP}=\frac{3}{4}\times S_{ANC}\)(chung đường cao hạ từ \(N\), \(AP=\frac{3}{4}\times AC\))
Suy ra \(S_{ANP}=\frac{3}{4}\times\frac{1}{2}\times S_{ABC}=\frac{3}{8}\times S_{ABC}\)
Ta có: \(S_{MQPN}=S_{ANP}-S_{AMQ}=\frac{3}{8}\times S_{ABC}-\frac{1}{8}\times S_{ABC}=\frac{1}{4}\times S_{ABC}=505\left(cm^2\right)\)