giải chi tiết luôn
K
Khách
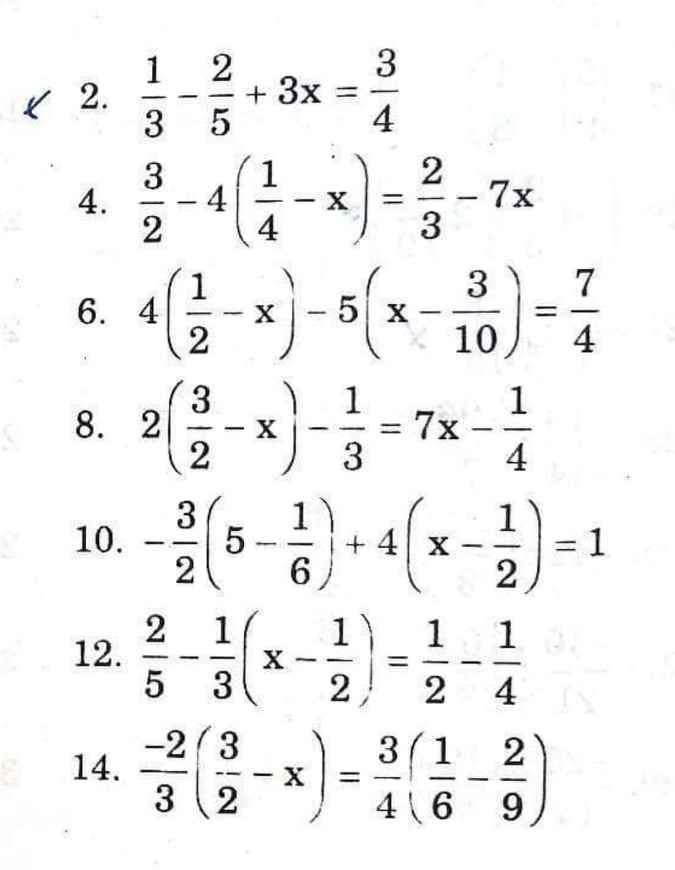
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 11 2021
\(=7\sqrt{a}+6b\cdot5a\sqrt{a}+5a\cdot6\left(-b\right)\sqrt{a}-4\sqrt{a}=3\sqrt{a}+30ab\sqrt{a}-30ab\sqrt{a}=3\sqrt{a}\left(B\right)\)
H
19 tháng 7 2021
a)
$n_{Nito} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{Nito} = 1.14 = 14(gam)$
b)
$n_{Cl} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{Cl} = 1.35,5 = 35,5(gam)$
c)
$n_{H_2O} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{H_2O} = 1.18 = 18(gam)$
TP
19 tháng 7 2021
a) \(n_{N_2}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{N_2}=1.28=28\left(g\right)\)
b) \(n_{Cl_2}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{Cl_2}=1.35,5.2=71\left(g\right)\)
c) \(n_{H_2O}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{H_2O}=1.18=18\left(g\right)\)
d) \(n_{CaCO_3}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{CaCO_3}=1.100=100\left(g\right)\)
8 tháng 2 2023
Đặt (P): F(x)=ax^2+bx+c
Vì (P) đi qua (0;-3); (5;2); đỉnh là (2;-7) nên ta có hệ:
\(\left\{{}\begin{matrix}a\cdot0^2+b\cdot0+c=-3\\25a+5b+c=2\\\left\{{}\begin{matrix}\dfrac{-b}{2a}=2\\-\dfrac{b^2-4ac}{4a}=-7\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}c=-3\\25a+5b=5\\b=-4a\\b^2-4ac=28a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=-3\\a=1\\b=-4\end{matrix}\right.\)
=>(P): F(x)=x^2-4x-3
Đặt (H): G(x)=ax^2+bx+c
G(x) đi qua (3;0); (-1;0); đỉnh là I(1;4)
=>Hệ pt:
\(\Leftrightarrow\left\{{}\begin{matrix}a\cdot3^2+b\cdot3+c=0\\a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=0\\\dfrac{-b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9a+3b+c=0\\a-b+c=0\\b=-2a\\\dfrac{b^2-4ac}{4a}=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8a+4b=0\\b+2a=0\\a-b+c=0\\b^2-4ac=-16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\a+2a+c=0\\b^2-4ac=-16a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=-3a\\\left(-2a\right)^2-4a\cdot\left(-3a\right)=-16a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2+12a+16a=0\\b=-2a\\c=-3a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-7\\b=14\\c=21\end{matrix}\right.\)
=>(H): G(x)=49x^2+14x+21
F(x): x^2-4x-3
=>Ko có câu nào đúng
2T
1
LP
Lê Phương Thảo
Giáo viên
17 tháng 3 2022
nKMnO4 = 14,2/158 ≃ 0,0899 mol
2KMnO4 + 16HCl → 2KCl + 2MnCl2 + 5Cl2 + 8H2O
0,0899 \(\dfrac{0,0899\times5}{2}\)
→ nCl2 = 0,22475 mol → VCl2 = 22,4.nCl2 = 5,0344 lít
NV
2
9P
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2022
ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)
2.
\(\dfrac{1}{3}-\dfrac{2}{5}+3x=\dfrac{3}{4}\\ \text{⇔}-\dfrac{1}{15}+3x=\dfrac{3}{4}\\ \text{⇔}3x=\dfrac{3}{4}+\dfrac{1}{15}=\dfrac{49}{60}\\ \text{⇔}x=\dfrac{49}{180}\)
4.
\(\dfrac{3}{2}-4\left(\dfrac{1}{4}-x\right)=\dfrac{2}{3}-7x\\ \text{⇔}\dfrac{3}{2}-1+4x=\dfrac{2}{3}\\ \text{⇔}4x+\dfrac{1}{2}=\dfrac{2}{3}\\ \text{⇔}4x=\dfrac{1}{6}\\ \text{⇔}x=\dfrac{1}{24}\)
6.
\(4\left(\dfrac{1}{2}-x\right)-5\left(x-\dfrac{3}{10}\right)=\dfrac{7}{4}\\ \text{⇔}2-4x-5x+\dfrac{15}{10}=\dfrac{7}{4}\\ \text{⇔}\dfrac{7}{2}-9x=\dfrac{7}{4}\\ \text{⇔}9x=\dfrac{7}{4}\\ \text{⇔}x=\dfrac{7}{36}\)
8.
\(3-2x-\dfrac{1}{3}=7x-\dfrac{1}{4}\\ \text{⇔}9x-\dfrac{35}{12}=0\\ \text{⇔}x=\dfrac{35}{108}\)
10.
\(-\dfrac{15}{2}+\dfrac{1}{4}+4x-2=1\\ \text{⇔}4x=\dfrac{41}{4}\\ \text{⇔}x=\dfrac{41}{16}\)
12.
\(\dfrac{2}{5}-\dfrac{1}{3}x+\dfrac{1}{6}=\dfrac{1}{4}\\ \text{⇔}\dfrac{17}{30}-\dfrac{1}{3}x=\dfrac{1}{3}\\ \text{⇔}\dfrac{1}{3}x=\dfrac{7}{30}\\ \text{⇔}x=\dfrac{7}{10}\)
14.
\(-1+\dfrac{2}{3}x=\dfrac{1}{8}-\dfrac{1}{6}\\ \text{⇔}\dfrac{2}{3}x=\dfrac{23}{24}\\ \text{⇔}x=\dfrac{23}{16}\)
giúp với :(((