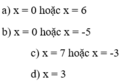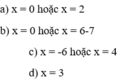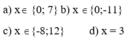tìm x biết: (x+7) . (x-3) < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NB
5
27 tháng 7 2017
x^2 -2x = 24
=> x^2 - 2x - 24=0
=>x^2 -8x+6x - 24 = 0
=> ( x^2- 8x)+( 6x-24) = 0
=> x(x-8) + 6(x-8) = 0
=> (x+6)(x-8)=0
=>\(\orbr{\begin{cases}x=-6\\x=8\end{cases}}\)
TN
19 tháng 7 2017
a) 2y - 12y = 0
\(\Rightarrow\) y ( 2-12) = 0
\(\Rightarrow\) y . (-10) =0
\(\Rightarrow\) y = 0 : (-10) = 0
b) (y-7)(y-8) = 0
\(\Rightarrow\orbr{\begin{cases}y-7=0\\y-8=0\end{cases}\Rightarrow\orbr{\begin{cases}y=0+7\\y=0+8\end{cases}\Rightarrow}\orbr{\begin{cases}y=7\\y=8\end{cases}}}\)
c) x + x.2+x.3+x.4+...+x.10 = 165
\(\Rightarrow\) x ( 1+2+3+.....+8+9+10) = 165
\(\Rightarrow\)x . \(\frac{\left(1+10\right).10}{2}\)=165
\(\Rightarrow\) x . 55 = 165
\(\Rightarrow x=\frac{165}{55}=3\)
Can you k for me ,Lê Thị Kim Chi!
N
19 tháng 7 2017
a) \(2y-12y=0\)
\(\Leftrightarrow-10y=0\)
\(\Leftrightarrow y=0:\left(-10\right)\)
\(\Leftrightarrow y=0\)
b) \(\left(y-7\right)\left(y-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y-7=0\\y-8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=0+7\\y=0+8\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}y=7\\y=8\end{cases}}\)
c) \(x+x.2+x.3+......+x.10=165\)
\(\Leftrightarrow x.\left(1+2+3+.....+10\right)=165\)
\(\Leftrightarrow x.55=165\)
\(\Leftrightarrow x=165:55\)
\(\Leftrightarrow x=3\)
CU
16 tháng 2 2019
(-x + 5)(3 - x) = 0
=> -x +5 = 0 và 3 - x = 0
=> -x = -5 và x = 3
=> x = 5 hoặc x = 3
x(2 + x)(7-x) = 0
=> x = 0 hoặc 2 + x =0 và 7 - x = 0
=> x = 0 hoặc x = -2 hoặc x = 7
16 tháng 2 2019
Câu 1:
\(\Leftrightarrow\orbr{\begin{cases}-x+5=0\\3-x=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}-x=-5\\x=3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=3\end{cases}}\)
Vậy \(x\in3;5\)
Câu 2:
Cách giải tương tự: Cho từng thừa số =0 rồi giải ra sẽ được:
\(x\in0;-2;7\)
18 tháng 2 2020
Các bạn giúp mình giải với nhé! Đúng thì mình k đúng nhé. Cảm ơn các bạn nhiều lắm. Yêu cả nhà.
28 tháng 2 2021
\(1.\left(x-5\right)^{23}.\left(y+2\right)^7=0\)
\(\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0\\\left(y+2\right)^7=0\end{cases}\Rightarrow\hept{\begin{cases}\left(x-5\right)^{23}=0^{23}\\\left(y+2\right)^7=0^7\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x-5=0\\y+2=0\end{cases}\Rightarrow\hept{\begin{cases}x=0+5\\y=0-2\end{cases}}}\)\(\Rightarrow\hept{\begin{cases}x=5\\y=-2\end{cases}}\)
Vậy \(\left(x;y\right)=\left(5;-2\right)\)
DT
Dang Tung
CTVHS
16 tháng 6 2023
\(\left(a\right):2x-7\sqrt{x}+3=0\left(x\ge0\right)\\ < =>\left(2x-6\sqrt{x}\right)-\left(\sqrt{x}-3\right)=0\\ < =>2\sqrt{x}\left(\sqrt{x}-3\right)-\left(\sqrt{x}-3\right)=0\\ < =>\left(2\sqrt{x}-1\right)\left(\sqrt{x}-3\right)=0\\ =>\left[{}\begin{matrix}2\sqrt{x}-1=0\\\sqrt{x}-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{1}{4}\left(TM\right)\\x=9\left(TM\right)\end{matrix}\right.\)
\(\left(b\right):3\sqrt{x}+5< 6\\ < =>3\sqrt{x}< 1\\ < =>\sqrt{x}< \dfrac{1}{3}\\ < =>0\le x< \dfrac{1}{9}\)
\(\left(c\right):x-3\sqrt{x}-10< 0\\ < =>\left(x-5\sqrt{x}\right)+\left(2\sqrt{x}-10\right)< 0\\ < =>\sqrt{x}\left(\sqrt{x}-5\right)+2\left(\sqrt{x}-5\right)< 0\\ < =>\left(\sqrt{x}-5\right)\left(\sqrt{x}+2\right)< 0\\ =>\left\{{}\begin{matrix}\sqrt{x}-5< 0\\\sqrt{x}+2>0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}0\le x< 25\\x\ge0\end{matrix}\right.< =>0\le x< 25\)
\(\left(d\right):x-5\sqrt{x}+6=0\left(x\ge0\right)\\ < =>\left(x-2\sqrt{x}\right)-\left(3\sqrt{x}-6\right)=0\\ < =>\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)=0\\ < =>\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)=0\\ =>\left[{}\begin{matrix}\sqrt{x}-3=0\\\sqrt{x}-2=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=9\\x=4\end{matrix}\right.\left(TM\right)\)
\(\left(e\right):x+5\sqrt{x}-14< 0\\ < =>\left(x+7\sqrt{x}\right)-\left(2\sqrt{x}+14\right)< 0\\ < =>\sqrt{x}\left(\sqrt{x}+7\right)-2\left(\sqrt{x}+7\right)< 0\\ < =>\left(\sqrt{x}-2\right)\left(\sqrt{x}+7\right)< 0\\ =>\left\{{}\begin{matrix}\sqrt{x}+7>0\\\sqrt{x}-2< 0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x\ge0\\0\le x< 4\end{matrix}\right.< =>0\le x< 4\)