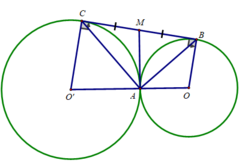
Cho đường tròn (O,R) tiếp xúc ngoài với (O’,r) tại A. Một tiếp tuyến chung ngoài của hai đường tròn (O) và (O’) lần lượt tiếp xúc với hai đường tròn tại B và C. Vẽ AH vuông góc với BC tại H
a) Tính BC theo R và r
b) Chứng minh rằng ba đường thẳng OB, O’C và AH đồng qui tại trung điểm của AH