Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Vì 2-căn 3>0 nên số này có căn bậc hai số học
b: Vì 4-căn 15>0 nên số này có căn bậc hai số học
c: Vì \(2\sqrt{3}-\sqrt{6}-1>0\)
nên số này có căn bậc hái số học
d: \(3\sqrt{2}-2\sqrt{5}+1>0\)
nên số này có căn bậc hai số học
Lời giải:
Một số không âm thì sẽ có căn bậc 2 số học nên chỉ cần chứng minh biểu thức không âm là được
1.
$2-\sqrt{3}=\sqrt{4}-\sqrt{3}>0$ nên biểu thức có CBHSH
2.
$4-\sqrt{15}=\sqrt{16}-\sqrt{15}>0$ nên biểu thức có CBHSH
3.
$(2\sqrt{3})^2=12$
$(\sqrt{6}+1)^2=7+2\sqrt{6}=7+\sqrt{24}< 7+\sqrt{25}=12$
$\Rightarrow (2\sqrt{3})^2>(\sqrt{6}+1)^2\Rightarrow 2\sqrt{3}>\sqrt{6}+1$
$\Rightarrow 2\sqrt{3}-\sqrt{6}-1>0$ nên có CBHSH
4.
$(2\sqrt{5})^2=20$
$(3\sqrt{2}+1)^2=19+6\sqrt{2}>19+1=20$
$\Rightarrow (2\sqrt{5})^2< (3\sqrt{2}+1)^2\Rightarrow 2\sqrt{5}< 3\sqrt{2}+1$
$\Rightarrow 3\sqrt{2}-2\sqrt{5}+1>0$ nên có CBHSH
5.
$\sqrt{26}>\sqrt{25}=5$
$\sqrt{37}>\sqrt{36}=6$
$\Rightarrow 11-\sqrt{26}-\sqrt{37}=(5-\sqrt{26})+(6-\sqrt{37})< 0$ nên không có CBHSH
6.
$\sqrt{26}>\sqrt{25}=5$
$\sqrt{17}>\sqrt{16}=4$
$\Rightarrow \sqrt{26}+\sqrt{17}+1>10=\sqrt{100}>\sqrt{99}$
$\Rightarrow \sqrt{26}+\sqrt{17}+1-\sqrt{99}>0$ nên có CBHSH
Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
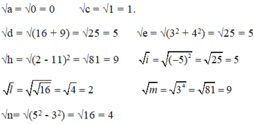
Không phải là căn bậc hai số học là đứng độc lập 1 mình đâu bạn
Những trường hợp em nêu đều là CBHSH
$2\sqrt{3}$ là căn bậc 2 số học của $12$
$\sqrt{3}.\sqrt{4}$ là căn bậc 2 số học của $12$
$\sqrt{\frac{3}{4}}$ là căn bậc 2 số học $\frac{3}{4}$
Em cứ nhớ $\sqrt{x}$ (với $x$ là số không âm) là CBHSH của $x$, dù nó biểu diễn kiểu gì đi chăng nữa.
Bạn chỉ cần hiểu là căn bậc hai số học của là một số x sao cho \(x^2=a\) và \(x\ge0\) thôi
a: 12 là căn bậc hai số học của 144
b: -0,36 không là căn bậc hai số học của bất kỳ số thực nào
c: \(\dfrac{2\sqrt{2}}{7}\) là căn bậc hai số học của \(\dfrac{8}{49}\)
