cho TAM GIÁC ABC, AN=1/3 NM, BN=BP,CP gấp 3 lần CM, BIẾT DIỆN TÍCH TAM GIÁC MNP= 200 CM2. TÍNH DIEN TÍCH ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 7 2023
AM=1/3AO
=>OM=2/3AO
BN=1/3BO
=>ON/OB=2/3
CP=1/3CO
=>OP/OC=2/3
Xét ΔOAC có OM/OA=OP/OC
nên MP//AC và MP/AC=OM/MA
=>ΔOMP đồng dạng với ΔOAC
=>S OMP/S OAC=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOAB có OM/OA=ON/OB
nên MN//AB
=>ΔOMN đồng dạng với ΔOAB
=>S OMN/S OAB=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOBC có ON/OB=OP/OC
nên NP//BC
=>ΔONP đồng dạng với ΔOBC
=>S ONP/S OBC=(ON/OB)^2=4/9
=>S MNP=4/9*S ABC=40cm2
25 tháng 6 2023
Cho tui tick nha
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 6 2023
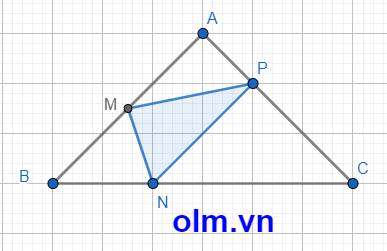
SAMP = \(\dfrac{1}{2}\)SABP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
AP = AC - PC = AC - \(\dfrac{2}{3}\) AC = \(\dfrac{1}{3}\)AC
SAPB = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và AP = \(\dfrac{1}{3}\) AC)
⇒ SAMP = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
SBMN = \(\dfrac{1}{2}\)SABN (vì hai tam giác có chung chiều cao hạ từ đỉnh N xuống đáy AB và BM = \(\dfrac{1}{2}\) AB)
SABN = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BN = \(\dfrac{1}{3}\)BC)
SBMN = \(\dfrac{1}{2}\times\) \(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC
SCNP = \(\dfrac{2}{3}\)SBCP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{2}{3}\) BC)
SBCP = \(\dfrac{2}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và PC = \(\dfrac{2}{3}\)CA)
SCNP = \(\dfrac{2}{3}\times\dfrac{2}{3}\) = \(\dfrac{4}{9}\)\(\times\)36 = 16 (cm2)
Diện tích tam giác MNP là:
36 - (6+6+16) = 8 (cm2)
Đáp số: 8 cm2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
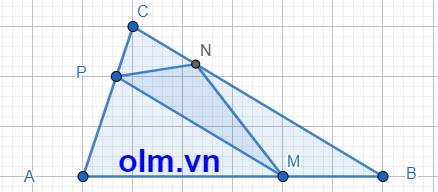
AP = AC - PC = AC - \(\dfrac{1}{3}\)AC = \(\dfrac{2}{3}\)AC
SAMP = \(\dfrac{2}{3}\)SACM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy AC và AP = \(\dfrac{2}{3}\)AC)
SACM = \(\dfrac{2}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và AM = \(\dfrac{2}{3}\)AB)
SAMP = \(\dfrac{2}{3}\times\dfrac{2}{3}\)SABC = 180 \(\times\dfrac{4}{9}\) = 80 (cm2)
SBMN = \(\dfrac{3}{4}\)SBCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{3}{4}\)BC)
BM = AB - AM = AB - \(\dfrac{2}{3}\)AB = \(\dfrac{1}{3}\)AB
SBCM = \(\dfrac{1}{3}\)SABC( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{1}{3}\)AB)
SBMN = \(\dfrac{3}{4}\times\dfrac{1}{3}\)SABC = 180 \(\times\dfrac{1}{4}\) = 45 (cm2)
CN = BC - BN = BC - \(\dfrac{3}{4}\)BC = \(\dfrac{1}{4}\)BC
SCPN = \(\dfrac{1}{4}\)SCPB ( vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{4}\)BC)
SCBP = \(\dfrac{1}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và CP = \(\dfrac{1}{3}\)CA)
SCPN = \(\dfrac{1}{4}\times\dfrac{1}{3}\)SABC = 180 \(\times\) \(\dfrac{1}{12}\) = 15 (cm2)
Diện tích tam giác MNPQ là:
180 - ( 80 + 45 + 15) = 40 (cm2)
Đáp số 40 cm2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 6 2023
\(\dfrac{CP}{CA}=\dfrac{2}{3}\Rightarrow\dfrac{AP}{CA}=\dfrac{1}{3}\)
Hai tg ABP và tg ABC có chung đường cao từ B->CA nên
\(\dfrac{S_{ABP}}{S_{ABC}}=\dfrac{AP}{CA}=\dfrac{1}{3}\Rightarrow S_{ABP}=\dfrac{1}{3}xS_{ABC}\)
Hai tg AMP và tg ABP có chung đường cao từ P->AB nên
\(\dfrac{S_{AMP}}{S_{ABP}}=\dfrac{AM}{AM}=\dfrac{1}{4}\Rightarrow S_{AMP}=\dfrac{1}{4}xS_{ABP}=\dfrac{1}{4}x\dfrac{1}{3}xS_{ABC}=\dfrac{1}{12}xS_{ABC}\)
\(S_{BCP}=S_{ABC}-S_{ABP}=S_{ABC}-\dfrac{1}{3}xS_{ABC}=\dfrac{2}{3}xS_{ABC}\)
\(\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow\dfrac{CN}{BC}=\dfrac{1}{3}\)
Hai tg CNP và tg BCP có chung đường cao từ P->BC nên
\(\dfrac{S_{CNP}}{S_{BCP}}=\dfrac{CN}{BC}=\dfrac{1}{3}\Rightarrow S_{CNP}=\dfrac{1}{3}xS_{BCP}=\dfrac{1}{3}x\dfrac{2}{3}xS_{ABC}=\dfrac{2}{9}xS_{ABC}\)
\(\dfrac{AM}{AB}=\dfrac{1}{4}\Rightarrow\dfrac{BM}{AB}=\dfrac{3}{4}\)
Hai tg BCM và tg ABC có chung đường cao từ C->AB nên
\(\dfrac{S_{BCM}}{S_{ABC}}=\dfrac{BM}{AB}=\dfrac{3}{4}\Rightarrow S_{BCM}=\dfrac{3}{4}xS_{ABC}\)
Hai tg BMN và tg BCM có chung đường cao từ M->BC nên
\(\dfrac{S_{BMN}}{S_{BCM}}=\dfrac{BN}{BC}=\dfrac{2}{3}\Rightarrow S_{BMN}=\dfrac{2}{3}xS_{BCM}=\dfrac{2}{3}x\dfrac{3}{4}xS_{ABC}=\dfrac{1}{2}xS_{ABC}\)
\(S_{MNP}=S_{ABC}-S_{AMP}-S_{CNP}-S_{BMN}=\)
\(=S_{ABC}-\dfrac{1}{12}xS_{ABC}-\dfrac{2}{9}xS_{ABC}-\dfrac{1}{2}xS_{ABC}=\)
\(=\dfrac{11}{36}xS_{ABC}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
cô làm rồi em nhé
https://olm.vn/cau-hoi/cho-tam-giac-abc-co-dien-tich-180-cm2-tren-cac-canh-ab-bc-ca-lan-luot-lay-cac-diem-m-n-p-sao-cho-am-23-ab-bn-34-bc-va-cp-13-ca-tinh-di.8088189515587