Cho tam giác ABC vuông tại A có BC=6cm ,AB=2AC . tính diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 2 2021
1) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
2) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
3) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
CM
2 tháng 9 2019
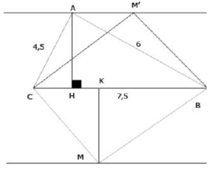
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
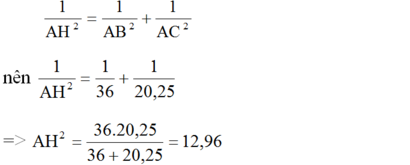
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8 2023
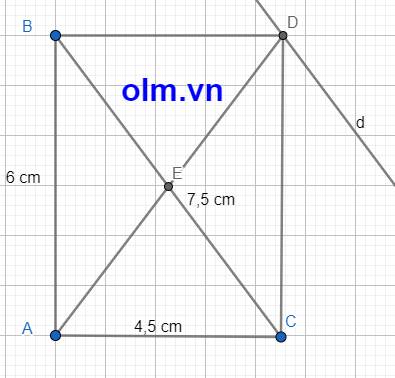
a, Xét \(\Delta\)ABC có: AB2 + AC2 = 62 + 4,52 = 56,25 (cm2)
BC2 = 7,52 = 56,25 (cm2)
AB2 + AC2 = BC2 vậy tam giác ABC vuông tại A (đpcm)
SinC = 6 : 7,5 =0,8 ⇒ \(\widehat{C}\) = 53,130 ⇒ \(\widehat{B}\) = 900 - 53,130 = 36,870
b, Dựng hình chữ nhật ABCD, chiều cao AH, DK, và đường thẳng d đi qua D song song với BC như hình vẽ ta có
SABC = SBDC ⇒ AH = DK
Lây 1 điểm bất M kỳ di động trên đường thẳng d ta có:
SBDC = SMBC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy BC)
⇒ SABC = SMBC
Kết luận khi M di động trên đường thẳng d thì diện tích tam giác MBC luôn bằng diện tích tam giác ABC
19 tháng 9 2021
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
TT
13 tháng 11 2020
a) Diện tích tam giác ABC (Heron)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(AB+BC+AC\right)\left(AB+BC-AC\right)\left(BC+AC-AB\right)\left(AC+AB-BC\right)}\)
\(S_{ABC}=\frac{1}{4}\sqrt{\left(6+10+8\right)\left(6+10-8\right)\left(10+8-6\right)\left(8+6-10\right)}=24\left(cm^2\right)\)
b)Xét tam giác ABC có
\(BC^2=10^2=100\left(cm\right)\)
\(AB^2+AC^2=6^2+8^2=100\left(cm\right)\)
Vì 100cm=100cm
\(\Rightarrow BC^2=AB^2+AC^2\)
=> Tam giác ABC vuông tại A
Xét diện tích tam giác ABC thường \(S_{ABCt}=\frac{AH.BC}{2}\left(1\right)\)
Xét diện tích tam giác ABC vuông \(S_{ABCv}=\frac{AC.AB}{2}\left(2\right)\)
Từ (1) và (2)
\(\Leftrightarrow AH.BC=AB.AC\)
\(\Leftrightarrow AH.10=8.6\Leftrightarrow AH=4,8\left(cm\right)\)
Xét tam giác ABH vuông tại H
\(\Rightarrow BH^2=AB^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}\)
\(\Rightarrow BH=\sqrt{6^2-13,3^2}=3,6\left(cm\right)\)
Xét tam giác ACH vuông tại H
\(\Rightarrow HC^2=AC^2-AH^2\left(PYTAGO\right)\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{8^2-4,8^2}=6,4\left(cm\right)\)
8 tháng 1 2022
a) \(\Delta ABC\) vuông tại A (gt).
\(\Rightarrow S_{\Delta ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}6.8=24\left(cm^2\right).\)
b) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2.\Rightarrow BC^2=6^2+8^2.\Leftrightarrow BC^2=36+64=100.\)
\(\Rightarrow BC=10\left(cm\right).\)
c) Ta có: \(S_{\Delta ABC}=\dfrac{1}{2}AH.BC.\)
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.\)
\(\Rightarrow\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC.\)
\(\Rightarrow\dfrac{1}{2}AH.10=24.\Leftrightarrow AH=4,8\left(cm\right).\)
8 tháng 1 2022
a)Diện tích tam giác vuông ABC là:
S=1/2* AB *AC = 1/2 * 6 * 8= 24 (cm2)
b)Độ dài cạnh BC là:
theo định lý pytago về tam giác vuông, ta có
BC2= AB2+AC2= 62 + 82 = 100 cm => BC = \(\sqrt{100}\) = 10cm
c) Độ dài đường cao AH
AC2= BC*HC => HC = \(\dfrac{AC^2}{BC}\) = 6,4 cm
BH = BC - HC = 10 - 6,4 = 3,6 cm
AH2 = BH*HC = 6,4 * 3,6 = \(\dfrac{576}{25}\) => AH = \(\sqrt{\dfrac{576}{25}}=4,8cm\)
DT
8 tháng 1 2022
a,
\(S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{6.8}{2}=24cm^2\)
b. \(BC^2=AB^2+AC^2\Rightarrow BC=10cm\)
8 tháng 1 2022
c: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8cm
GT
16 tháng 1 2022
a)SABC=6.8=48(cm2)
b)Áp dụng định lý Py-ta-go trong tam giác vuông ABC có: BC=10cm
c)AB.AC=BC.AH =>AH=(AB.AC)/BC=4,8cm
Có tam giác ABC vuông tại A ( gt )
\(\Rightarrow\) BC\(^2\) = AB\(^2\) + AC\(^2\) ( định lý Pytago )
\(\Rightarrow\) BC\(^2\) = ( 2AC )\(^2\) + AC \(^2\)
\(\Rightarrow\) BC\(^2\) = 2\(^2\) . AC\(^2\) + AC\(^2\)
\(\Rightarrow\) BC\(^2\) = 5AC\(^2\)
Bạn làm tiếp phần còn lại nhé . Chúc bạn học tốt !
giair cách số số học gúp mk nha !