Trong màn đêm bao phủ lấy tôi
Vẫn còn một ánh sáng nhỏ nhoi
Tôi nên chọn ánh sáng đó
Hay ở lại với màn đêm?
Mn nhận xét bài thơ trên giúp mk với!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Khoảng vân i = λ D a
Cách giải:
+ Ban đầu: D 1 = D
Trên MN có n vân sáng = Đoạn MN = ( n - 1 ) i 1 (1)
+ Khi tịnh tiến màn nh theo hướng ra xa màn chắn thêm đoạn 50cm = 0,5m thì trên MN có có n - 2 vân sáng = Đoạn MN = ( n - 3 ) i 2 (2)
Ta có: i 1 = λ D a i 2 = λ ( D + 0,5 ) a
Từ (1) và (2), ta có:
( n − 1 ) i 1 = ( n − 3 ) i 2 ↔ ( n − 1 ) λ D a = ( n − 3 ) λ ( D + 0,5 ) a → ( n − 1 ) D = ( n − 3 ) ( D + 0,5 ) → n = 4 D + 3
Thay vào (1) ta được: M N = n − 1 i 1 = ( n − 1 ) λ D a = ( 4 D + 3 − 1 ) D λ a = 12 m m
↔ ( 4 D + 2 ) D = 20 → D = 2 D = − 2,5 ( l o a i ) ⇒ D = 2 m

Phương pháp:
Sử dụng lí thuyết về bài toán trùng nhau của 2 bức xạ trong giao thoa sóng ánh sáng
Hai bức xạ trùng nhau: x1 = x2 <=> k1.λ1 = k2.λ2
Cách giải:
+ Ta có: i1 = 0,6 mm và i2 = 0,78 mm
+ Vị trí hai bức xạ trùng nhau:
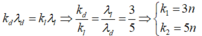

+ Số vân sáng của λ 1 = 500 nm trên đoạn MN là:
![]()
có 10 giá trị
+ Số vân sáng của λ 2 = 650 nm trên đoạn MN là:
![]()
có 8 giá trị
+ Số vân sáng trùng của hai bức xạ trên đoạn MN là:
![]()
có 1 giá trị
+ Số vân sáng quan sát được là: N = N1 + N2 – N0 = 17
Chọn B

Đáp án B
+ Khoảng vân giao thoa của các ánh sáng đơn sắc

+ Ta xét các tỉ số:
x M i 1 = 3 , 3 x M i 1 = 13 , 3 → trên đoạn MN có các vị trí cho vân sáng từ bậc 4 đến bậc 13 của bức xạ λ1
x M i 2 = 2 , 56 x M i 2 = 10 , 25 → trên đoạn MN có các vị trí cho vân sáng từ bậc 3 đến bậc 10 của bức xạ λ2
+ Điều kiện trùng nhau của hai hệ vân
λ 1 λ 2 = k 2 k 1 = 10 13 → trên đoạn MN có một vị trí trùng nhau của hệ hai vân sáng, do đó số vân sáng quan sát được là
n
=
10
+
8
-
1
=
17
(ta trừ một là do hai vân sáng trùng nhau ta tính là một vân sáng)
mik thấy bài thơ
nó cứ sao ấy
ko có vần , các tiếng ko hòa hợp vs nhau
mik xin lỗi
Bài này ko có vần liền
Ko nhịp điệu