Tìm x, biết: x(x2−3)=9+x3.
Giá trị của x cần tìm là ...........
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TD
2
Những câu hỏi liên quan
28 tháng 7 2023
2:
a: =>(x-9)(x-1)=0
=>x=9 hoặc x=1
b: =>(x+4)(x^2-4x+16)+(x+4)(x-16)=0
=>(x+4)(x^2-4x+16+x-16)=0
=>(x+4)(x^2-3x)=0
=>x(x-3)(x+4)=0
=>x=0;x=3;x=-4
YN
28 tháng 7 2023
bài 2 :
a: =>(x-9)(x-1)=0
=>x=9 hoặc x=1
b: =>(x+4)(x^2-4x+16)+(x+4)(x-16)=0
=>(x+4)(x^2-4x+16+x-16)=0
=>(x+4)(x^2-3x)=0
=>x(x-3)(x+4)=0
=>x=0;x=3;x=-4
23 tháng 12 2022
a ĐKXĐ: x<>0; x<>3
b: Sửa đề; x^2-6x+9/x^2-3x
\(A=\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}=\dfrac{x-3}{x}\)
c: Khi x=5 thì \(A=\dfrac{5-3}{5}=\dfrac{2}{5}\)
PT
1
CM
16 tháng 8 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 1
Ta có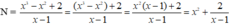 
Để N nguyên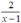 
nguyên ⇒ x - 1 là ước của 2
Ư ( 2 ) = 1 ; - 1 ; 2 ; - 2
x – 1 = 1 ⇒ x =2 (thỏa mãn điều kiện xác định);
x - 1 = -1 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x - 1 = 2 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x - 1 = -2 ⇒ x = -1 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -1;0;2;3 } thì phân thức N nhận giá trị nguyên
3 tháng 8 2023
a) \(\left(x-5\right)^2=\left(3+2x\right)^2\)
\(\Rightarrow\left(3+2x\right)^2-\left(x-5\right)^2=0\)
\(\Rightarrow\left(3+2x+x-5\right)\left(3+2x-x+5\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(x+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x-2=0\\x+8=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-8\end{matrix}\right.\)
b) \(27x^3-54x^2+36x=9\)
\(\Rightarrow27x^3-54x^2+36x-9=0\)
\(\Rightarrow27x^3-54x^2+36x-8+8-9=0\)
\(\Rightarrow\left(3x-2\right)^3-1=0\)
\(\Rightarrow\left(3x-2-1\right)\left[\left(3x-2\right)^2+3x-2+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2\right)^2+3x-2+\dfrac{1}{4}-\dfrac{1}{4}+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\left(1\right)\)
mà \(\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0,\forall x\)
\(\left(1\right)\Rightarrow3x-3=0\Rightarrow3x=3\Rightarrow x=1\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 8 2023
(\(x-5\))2 = (3 +2\(x\))2 ⇒ \(\left[{}\begin{matrix}x-5=3+2x\\x-5=-3-2x\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\) vậy \(x\in\){-8; \(\dfrac{2}{3}\)}
27\(x^3\) - 54\(x^2\) + 36\(x\) = 9
27\(x^3\) - 54\(x^2\) + 36\(x\) - 8 = 1
(3\(x\) - 2)3 = 1 ⇒ 3\(x\) - 2 = 1 ⇒ \(x\) = 1
PT
22 tháng 4 2021
Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910
1 tháng 8 2023
10:
Vì n là số lẻ nên n=2k-1
Số số hạng là (2k-1-1):2+1=k(số)
Tổng là (2k-1+1)*k/2=2k*k/2=k^2 là số chính phương
11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc {1;5;13;65}
=>\(n\in\left\{0;2;-2;2\sqrt{3};-2\sqrt{3};8;-8\right\}\)
CM
3 tháng 10 2018
Đáp án A.
Tập xác định D = R.
y' = x2 – 2(m + 1)x + m2 – 3, y’’ = 2x – 2(m + 1).
Hàm số đạt cực trị tại x = -1
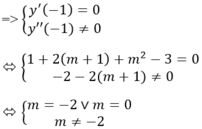
Vậy m = 0 thì hàm số đạt cực trị tại x = -1
$x(x^2-3)=9+x^3\\\Leftrightarrow x^3-3x=9+x^3\\\Leftrightarrow x^3-3x-x^3=9\\\Leftrightarrow -3x=9\\\Leftrightarrow x=-3$
Vậy giá trị của $x$ cần tìm là $x=-3$
\(x\cdot\left(x^2-3\right)=9+x^3\)
\(\Leftrightarrow x^3-3x=9+x^3\)
\(\Leftrightarrow x^3-x^3=9+3x\)
\(\Leftrightarrow9+3x=0\)
\(\Leftrightarrow3x=-9\)
\(\Leftrightarrow x=-3\)