Có bao nhiêu số xx thỏa mãn: ...
Đọc tiếp
Có bao nhiêu số thỏa mãn:
x9 =64x7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
1
16 tháng 4 2022
a: Ta có: 9,5<x<17,7
mà x là số nguyên
nên \(x\in\left\{10;11;12;...;17\right\}\)
Số số hạng thỏa mãn là 17-10+1=8(số)
b: Ta có: -1,23<x<2,5
mà x là số nguyên
nên \(x\in\left\{-1;0;1;2\right\}\)
=>Có 4 số thỏa mãn
CM
13 tháng 12 2017
Chọn B.
Gọi số phức cần tìm là z = a + bi.
Ta có ( 1 - 3i) z = ( 1 - 3i) ( a + bi)
= a + 3b - 3ai + bi = a + 3b + ( b - 3a) i
+ Do ( 1 - 3i) z là số thực nên b - 3a = 0 hay b = 3a
+ ta có 
⇔|a – 2 + (-b + 5)i| = 1
Hay ( a - 2) 2 + ( 5 - 3a) 2 = 1
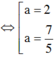(thỏa mãn)
Vậy có hai số phức z thỏa mãn là z = 2 + 6i và z = 7/5 + 21/5i
31 tháng 8 2019
Gọi năm đó là \(\overline{abcd}\). Vì chữ số liền sau không nhỏ hơn chữ số hàng liền trước, nên d là chữ số lớn nhất.
Ta có \(1\times2\times3=6\). Vậy d = 3, c = 2, b = 1.
Vì a không thể lớn hơn b nên a = 0 hoặc 1. Tuy nhiên số có 4 chữ số có hàng nghìn không bằng 0 \(\Rightarrow a=1\)
\(\Rightarrow\)Có một năm thỏa mãn điều kiện trên và năm đó là 1123
CM
21 tháng 11 2017
Chọn đáp án B
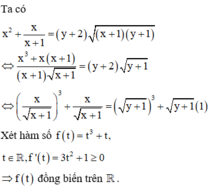
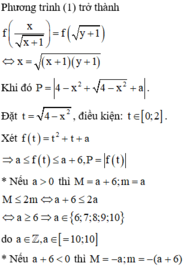
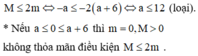
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
NL
0
Ta có : x9 = 64x7
=> x9 - 64x7 = 0
=> x7(x2 - 64) = 0
=> \(\orbr{\begin{cases}x^7=0\\x^2-64=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x^2=64\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x^2=8^2\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\pm8\end{cases}}\)
Vậy \(x\in\left\{0;8;-8\right\}\)là giá trị cần tìm hay có 3 số x thỏa mãn bài toán
\(x^9=64x^7\)
\(\Rightarrow\)\(64x^7=x^9\)
\(\Rightarrow\)\(x^9\div x^7=64\)
\(\Rightarrow\)\(x^2=64\)
\(\Rightarrow\)\(x^2=\left(\pm8\right)^2\)
\(\Rightarrow\)\(x=\pm8\)
Có 2 số x thỏa mãn.