Cho hình chữ nhật ABCD. E là một điểm thuộc cạnh AB. Đường thẳng DE cắt AC ở F, cắt CB ở G
a) Chứng minh tam giác BEG và tam giác CDG đồng dạng
b) Chứng minh \(FD^2=FE.FG\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
11 tháng 5 2016
Cô hướng dẫn nhé :)
a. \(\Delta AEF\sim\Delta CDF\left(g-g\right)\)
b. Ta thấy AB song song DC nên áp dụng Talet ta có:
\(\frac{EF}{FD}=\frac{AE}{DC}=\frac{1}{2}\)
Lại có: \(\Delta AED=\Delta BEG\left(g-c-g\right)\) nên ED = EG.
Ta thấy \(\frac{FD}{FG}=\frac{2EF}{EF+3EF}=\frac{1}{2}\)
\(\Rightarrow\frac{EF}{FD}=\frac{FD}{FG}\Rightarrow FD^2=EF.FG\)
C. Tính DE ta chỉ cần dùng định lý Pitago là xong rồi :)
Chúc em học tốt :))
4 tháng 7 2023
a: Xét ΔFAE vuông tại F và ΔFGC vuông tại F có
góc FAE=góc FGC
=>ΔFAE đồng dạng với ΔFGC
=>FA/FG=FE/FC
=>FA*FC=FE*FG=FD^2
b: DE=căn 18^2+24^2=30cm
Xét ΔEAD vuông tại A và ΔEBG vuông tại B có
EA=EB
góc AED=góc BEG
=>ΔEAD=ΔEBG
=>AD=BG=24cm và EG=ED=30cm
DG=30+30=60cm
NA
17 tháng 4 2022
$#Shả$
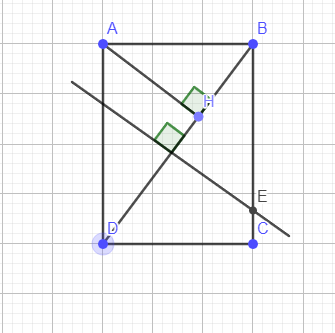
`a)` Xét `\triangleAHB` và `\triangleBCD` ta có `:`
`\hat{AHB}=\hat{BCD}=90^{o}`
`\hat{ABH}=\hat{BDC} ` (slt)
Vậy `\triangleAHB ` $\backsim$ `\triangleBCD` (g-g)
17 tháng 4 2022
a) △AHB và △BCD có: \(\widehat{AHB}=\widehat{BCD}=90^0\); \(\widehat{ABH}=\widehat{BDC}\) (AB//DC).
\(\Rightarrow\)△AHB∼△BCD (g-g).
b) △ABD có: \(BD^2=AD^2+AB^2\Rightarrow BD=\sqrt{AD^2+AB^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
△AHB∼△BCD \(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}=\dfrac{HB}{CD}\)
\(\Rightarrow\left[{}\begin{matrix}AH=\dfrac{AB.BC}{BD}=\dfrac{3.4}{5}=2,4\left(cm\right)\\HB=\dfrac{AB.CD}{BD}=\dfrac{3.3}{5}=1,8\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.2,4.1,8=2,16\left(cm^2\right)\)
c) ABCD là hình chữ nhật, AC cắt BD tại O.
\(\Rightarrow\)O là trung điểm của AC và BD.
BD⊥DE tại D, CF⊥DE tại F. \(\Rightarrow\)BD//CF.
-△ODE có: IF//OD \(\Rightarrow\dfrac{IF}{OD}=\dfrac{EI}{EO}\).
-△OBE có: IC//OB \(\Rightarrow\dfrac{IC}{OB}=\dfrac{EI}{EO}=\dfrac{IF}{OD}\Rightarrow IC=IF\Rightarrow\)I là trung điểm CF.
3 tháng 7 2022
a: XétΔAFE và ΔCFD có
góc AFE=góc CFD
góc FAE=góc FCD
Do đó: ΔAFE\(\sim\)ΔCFD
b: Xét ΔAFD và ΔCFG có
góc FDA=góc FGC
góc AFD=góc CFG
Do đó: ΔAFD đồng dạng với ΔCFG
=>FA/FC=FD/FG
hay FE/FD=FD/FG
hay \(FD^2=FE\cdot FG\)