Cho hình vẽ CMR: DA+DB<EA+EB<CA+CB A B C D E ...
Đọc tiếp
Cho hình vẽ CMR: DA+DB<EA+EB<CA+CB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2021
a: \(\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}\)
\(=\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{DA}+\overrightarrow{AD}\)
\(=\overrightarrow{0}\)
16 tháng 12 2023
A) Ta có:
- Tam giác ABQ vuông tại A nên AM là đường cao của tam giác ABQ.
- MB=MQ nên tam giác MBQ cân tại M.
- MD vuông góc với AB nên tam giác AMD vuông tại M.
- AH vuông góc với AQ nên tam giác AHQ vuông tại H.
- ME vuông góc với AQ nên tam giác AME vuông tại M.
Do đó, ta có:
- Tam giác ABQ và tam giác AMQ đồng dạng với nhau (cạnh góc cạnh).
- Tam giác MBQ và tam giác MDA đồng dạng với nhau (cạnh góc cạnh).
- Tam giác AME và tam giác MQE đồng dạng với nhau (cạnh góc cạnh).
Từ đó, ta có:
- $\frac{DE}{MQ}=\frac{AE}{AM}$ (đồng dạng tam giác AME và tam giác MQE)
- $\frac{AE}{AM}=\frac{AQ}{AB}$ (đồng dạng tam giác ABQ và tam giác AMQ)
- $\frac{AQ}{AB}=\frac{MD}{MB}$ (đồng dạng tam giác MBQ và tam giác MDA)
- $\frac{MD}{MB}=\frac{MA}{MQ}$ (đồng dạng tam giác MBQ và tam giác MDA)
Kết hợp các công thức trên, ta có:
$DE=\frac{MQ}{AM} \cdot AE=\frac{MQ}{AM} \cdot AQ \cdot \frac{MD}{MB}=\frac{MQ}{MA} \cdot MD$
Vì tam giác ABQ vuông tại A nên $MQ=\sqrt{AB^2-AH^2}$ và $MA=\frac{AB \cdot AH}{\sqrt{AB^2-AH^2}}$
Thay vào công thức trên, ta được:
$DE=\frac{\sqrt{AB^2-AH^2}}{AB \cdot AH} \cdot AB \cdot \frac{AB \cdot AH}{\sqrt{AB^2-AH^2}} \cdot MD=MD$
Vậy, ta có DE=MA.
B) Ta có:
- Tam giác ABQ vuông tại A nên AM là đường cao của tam giác ABQ.
- MB=MQ nên tam giác MBQ cân tại M.
- MD vuông góc với AB nên tam giác AMD vuông tại M.
- ME vuông góc với AQ nên tam giác AME vuông tại M.
Do đó, ta có:
- Tam giác ABQ và tam giác AMQ đồng dạng với nhau (cạnh góc cạnh).
- Tam giác MBQ và tam giác MDA đồng dạng với nhau (cạnh góc cạnh).
- Tam giác AME và tam giác MQE đồng dạng với nhau (cạnh góc cạnh).
Từ đó, ta có:
- $\frac{DE}{MQ}=\frac{AE}{AM}$ (đồng dạng tam giác AME và tam giác MQE)
- $\frac{AE}{AM}=\frac{AQ}{AB}$ (đồng dạng tam giác ABQ và tam giác AMQ)
- $\frac{AQ}{AB}=\frac{MD}{MB}$ (đồng dạng tam giác MBQ và tam giác MDA)
- $\frac{MD}{MB}=\frac{MA}{MQ}$ (đồng dạng tam giác MBQ và tam giác MDA)
Kết hợp các công thức trên, ta có:
$DE=\frac{MQ}{AM} \cdot AE=\frac{MQ}{AM} \cdot AQ \cdot \frac{MD}{MB}=\frac{MQ}{MA} \cdot MD$
Vì tam giác ABQ vuông tại A nên $MQ=\sqrt{AB^2-AH^2}$ và $MA=\frac{AB \cdot AH}{\sqrt{AB^2-AH^2}}$
Thay vào công thức trên, ta được:
$DE=\frac{\sqrt{AB^2-AH^2
16 tháng 12 2023
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
=>ADME là hình chữ nhật
=>DE=AM
b: Ta có: MD\(\perp\)AB
AQ\(\perp\)AB
Do đó:MD//AQ
Xét ΔBAQ có
M là trung điểm của BQ
MD//AQ
Do đó: D là trung điểm của AB
=>AD=DB
Ta có: AD=DB
AD=EM(ADME là hình chữ nhật)
Do đó: DB=EM
Xét tứ giác DBME có
DB//ME
DB=ME
Do đó: DBME là hình bình hành
CM
25 tháng 10 2017
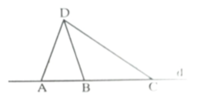
a) Có 3 tam giác đó là: tam giác DAB, tam giác DBC, tam giác DAC.
b) DB là cạnh của các tam giác DAB, DBC.
VA
7 tháng 5 2018
d) OD cat BE tai P D la truc tam cua tam giac BEO
=> OP vuong goc BE
Ta co AH//ME( cung vuong BM)=>DH/DM=AD/DE
ta co AF//PE( cung vuong OP)=>DF/DP=DH/DM =>DH/DM=DF/DP
tam giac DHF dong dang tam giacDMP (cgc) =>DHF=DMP => FH//MP(1)
AH//OM(cung vuong BM)=> BH/BM=BA/BO
AK//OP(cung vuong BE)=>BK/BP=BA/BO
=>BH/BM=BK/BP =>HK//MP( theo dltl dao)(2)
tu(1)(2)=> F H K thang hang
13 tháng 4 2020
Có 6 hình tâm giác Đó là ABH , BCH , CDH , AHC , BHD, AHD
Chúc bạn học tốt ~1
CM
8 tháng 1 2018
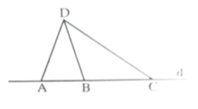
a) Có 3 tam giác đó là: tam giác DAB, tam giác DBC, tam giác DAC.