NA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 12 2017
a/ Xét \(\Delta ABD,\Delta ACD\)có:
\(AD\)(chung)
\(\widehat{BAD}=\widehat{CAD}\)
\(AB=AC\)
\(\Rightarrow\Delta ABD=\Delta ACD\)
\(\Rightarrow DB=DC\)
b/ Theo câu a thì ta có: \(\Rightarrow\Delta ABD=\Delta ACD\)
\(\Rightarrow\widehat{ADB}=\widehat{ADC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AD\perp BC\)
c/ Gọi M, N là giao điểm của AE với BF và BC
Xét \(\Delta BCF,\Delta ECA\) có
\(CE=CB\)
\(\widehat{ECA}=\widehat{BCF}=90^o+\widehat{BCA}\)
\(CA=CF\)
\(\Rightarrow\Delta BCF=\Delta ECA\)
\(\Rightarrow\widehat{FBC}=\widehat{AEC}\)
Mà \(\widehat{BNM}=\widehat{ENC}\)
\(\Rightarrow\widehat{BMN}=\widehat{ECN}=90^o\)
\(\Rightarrow EA\perp FB\)
19 tháng 11 2016
1/ Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OBD có:
OD: cạnh chung
\(\widehat{AOD}\)=\(\widehat{BOD}\) (GT)
OA = OB (GT)
Vậy tam giác OAD = tam giác OBD (c.g.c)
=> DA = DB (2 cạnh tương ứng)
b/ Ta có: tam giác OAD = tam giác OBD (câu a)
=> \(\widehat{ODA}\)=\(\widehat{ODB}\) (2 góc tương ứng)
Mà \(\widehat{ODA}\) + \(\widehat{ODB}\) = 1800 (kề bù)
=> \(\widehat{ODA}\)=\(\widehat{ODB}\) = \(\frac{1}{2}\)1800 = 900
=> OD \(\perp\)AB
Vậy OD vuông góc với AB
8 tháng 6 2016
Theo đề bài ta có:
a<b; c<d;e<f nên cộng vế với vế ta được:
a+c+e<b+d+f
<=>a+c+e+a+c+e<b+d+f+a+c+e
<=>2(a+c+e)<a+b+c+d+e+f
<=>\(\frac{a+c+e}{a+b+c+d+e+f}< \frac{1}{2}\)(ĐPCM)
VM
27 tháng 8 2019
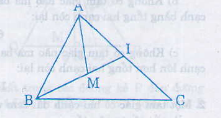
a) Ta có M nằm trong \(\Delta ABM.\)
=> \(A,M,I\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta AMI\) có:
\(AM< MI+IA\left(1\right).\)
b) Cộng vào hai vế của (1) với \(MB\) ta được:
\(AM+MB< MB+MI+IA\)
Mà \(MB+MI=IB.\)
=> \(AM+MB< BI+IA.\)
c) Ta có 3 điểm \(B,I,C\) không thẳng hàng.
Theo bất đẳng thức tam giác với \(\Delta BIC\) có:
\(BI< IC+BC.\) (2)
d) Cộng vào hai vế của (2) với \(IA\) ta được:
\(BI+IA< IA+IC+BC\)
Mà \(IA+IC=AC.\)
=> \(BI+IA< AC+BC.\)
e) Vì \(\left\{{}\begin{matrix}AM+MB< BI+IA\left(cmt\right)\\BI+IA< AC+BC\left(cmt\right)\end{matrix}\right.\)
=> \(AM+MB< AC+BC.\)
Chúc bạn học tốt!