Chứng minh Tam giác có 3 cạnh = nhau là tam giác đều , chứng minh tam có 2 góc = nhau là tam giác cân . " CTV giúp tao với "
P/S : đề chỉ dành cho học sinh giỏi nhé " CTV bơi hết vào đây "
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thằng thiểu năng, ai bảo m tam giác có 1 góc vuông thì không phải tam giác cân

Hình bạn tự vẽ nha
a) \(\Delta AEM\)vuông tại E có EI là trung tuyến
=> EI = IA (1) => \(\Delta EIA\)cân tại I, có EIM là góc ngoài
=> \(\widehat{EIM}=2\widehat{EAI}\)
Tương tự ta có \(\widehat{HIM}=2\widehat{HAI}\)và IH = IA (2)
Từ (1) và (2) suy ra IE = IH hay \(\Delta EIH\)cân tại I
có \(\widehat{EIH}=\widehat{EIM}+\widehat{HIM}=2\widehat{EAI}+2\widehat{HAI}=2\widehat{EAH}=2\left(90^o-\widehat{ABH}\right)=2\left(90^o-60^o\right)=60^o\)
Vậy EIH là tam giác đều, suy ra EI = EH = IH
Tương tự ta có IHF là tam giác đều, suy ra IH = HF = IF
=> EI = EH = IF = HF
Vậy HEIF là hình thoi
b) \(\Delta ABC\)là tam giac đều nên AH là đường cao cũng là đường trung tuyến
có G là trọng tâm nên \(AG=\frac{2}{3}AH\)(3)
Gọi K là trung điểm AG, suy ra \(AK=KG=\frac{1}{2}AG\)(4)
Từ (3) và (4) suy ra AK = KG = GH
Gọi O là giao điểm của EF và IH, suy ra OI = OH
\(\Delta AMG\)có IK là đường trung bình nên IK // MG
\(\Delta IKH\)có OG là đường trung bình nên IK // OG
=> M, O, G thẳng hàng (tiên đề Ơ-clit)
Vậy EF, MG, HI đồng quy
c) HEIF là hình thoi nên \(EF\perp HI\)
\(\Delta EIH\)đều có EO là đường cao nên \(EO=EI\sqrt{\frac{3}{4}}\)(bạn tự chứng minh)
\(EF=2EO=2EI\sqrt{\frac{3}{4}}=AM\sqrt{\frac{3}{4}}\)(5)
EF đạt GTNN khi AM đạt GTNN
mà \(AM\ge AH\)nên EF đạt GTNN khi M trùng H
Khi đó AM là đường cao trong tam giác đều ABC nên ta cũng có \(AM=AB\sqrt{\frac{3}{4}}=a\sqrt{\frac{3}{4}}\)(6)
Từ (5) và (6) suy ra \(EF=a\left(\sqrt{\frac{3}{4}}\right)^2=\frac{3}{4}a\)
Vậy EF đạt GTNN là \(\frac{3}{4}a\)khi M là chân đường cao hạ từ A xuống BC.
Ở đề không có điểm K, sao ở câu hỏi lại có điểm K vậy em?

t trả lời cho, khoi phải nhờ bọn CTV:
.
Do hình có từ vuông trong tên chắc chắn sẽ có it nhất 1 góc vuông ( trừ HCM )
Nên tam giác vuông là tam giác có 1 góc vuông.
.
m ngu à từ vuông có thể có nhiều góc vuông nhé chứ ko phải 1 sai rồi

* tam giác đều
- chứng minh tam giác có 3 cạnh = nhau
- chứng minh tam giác có 3 góc = nhau
- chứng minh tam giác có 2 góc = 60*
- chứng minh tam giác cân có 1 góc = 60*
Có tổng cộng 4 cách nha
ngoài 4 cách ấy ra,đang còn một cách nx đó là:2 đường cao vừa là phân giác vừa là trung tuyến
học tốt!

2) góc còn lại là 180 - 2.60=60
vậy 3 góc =60 độ => tam giác đều
1) 3 góc = nhau => 3*A=180 độ (gọi 3 góc là A,B,C)
=> a=60 độ = góc B = góc C

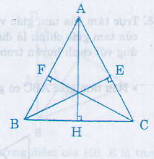
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.

a: Xét ΔDEA và ΔDFB có
DE=DF
góc D chung
DA=DB
=>ΔDEA=ΔDFB
b: ΔDEA=ΔDFB
=>góc DEA=góc DFB
=>góc KEF=góc KFE
=>ΔKEF cân tại K
c: ΔDEF cân tại D
mà DH là đường cao
nên DH là trung tuyến
=>DH,EA,FB đồng quy
Có phải là lớp 8 không vậy?
CMR: Tam giác có 3 cạnh bằng nhau là tam giác đều
Ta vẽ \(\Delta ABC\)có AB = AC = BC
Ta có AB = AC nên \(\Delta ABC\)cân tại A => \(\widehat{B}=\widehat{C}\)(1)
và AB = BC nên \(\Delta ABC\)cân tại B => \(\widehat{A}=\widehat{C}\)(2)
Từ (1) và (2) => \(\widehat{A}=\widehat{B}=\widehat{C}\)=> \(\Delta ABC\)đều (đpcm)
CMR: Tam giác có 2 cạnh bằng nhau là tam giác cân.
Ta vẽ \(\Delta ABC\)có AB = AC.
Kẻ AH \(\perp\)BC tại H.
\(\Delta AHB\)vuông và \(\Delta AHC\)vuông có: AB = AC (gt)
Cạnh AH chung
=> \(\Delta AHB\)vuông = \(\Delta AHC\)vuông (cạnh huyền - cạnh góc vuông) => \(\widehat{B}=\widehat{C}\)(hai góc tương ứng)
=> \(\Delta ABC\)cân tại A (đpcm)
huy hoàng t nói mãi mà mày éo hiểu ak ?
tại sao AB=AC thì suy ra ABC là tam giác cân " mày phải CM được AB=AC thì ABC là tam giác cân "