Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)
\( \Rightarrow \)MA = MC = \(\dfrac{1}{2}\)AC; NA = NB = \(\dfrac{1}{2}\)AB
Vì \(\Delta ABC\) cân tại A nên AB = AC ( tính chất)
Do đó, AM = MC = NA = NB
Xét \(\Delta \)ANC và \(\Delta \)AMB, ta có:
AN = AM
\(\widehat A\) chung
AC = AB
\( \Rightarrow \)\(\Delta \)ANC = \(\Delta \)AMB (c.g.c)
\( \Rightarrow \) NC = MB ( 2 cạnh tương ứng)
Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) ( tính chất đường trung tuyến trong tam giác)
Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
+) \(BC\) là cạnh chung
+) \(CN = BM\) (giả thiết)
+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.

#\(N\)
`a,` `GT: AB = AC,` \(\widehat{B}=\widehat{C}\)
`CM: BB' = C``C'`
`BB'` là đường trung tuyến
`-> B'` là trung điểm của `AC`
`-> AB' = B'C`
`C``C'` là đường trung tuyến
`-> C'` là trung điểm của `AB`
`-> AC' = C'B`
Tam giác `ABC` cân tại `A`
`-> AB = AC`
`-> AC' = AB' = C'B = B'C`
Xét Tam giác `BB'C` và Tam giác `C``C'B:`
`C'B = B'C`
\(\widehat{B}=\widehat{C}\)
`BC` chung
`=>` Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`=> BB' = C``C' (2` cạnh tương ứng `) (đpcm)`
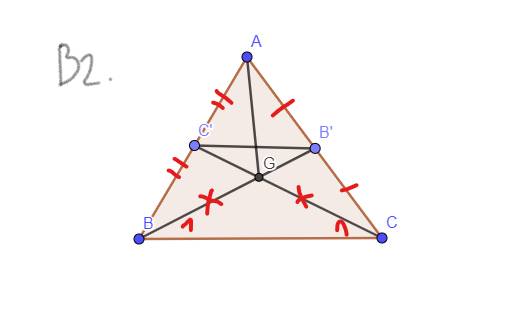
`b, GT: AB' = B'C ; AC'=C'B ; C``C' = BB'`
`KL:` Tam giác `ABC` cân
`BB', C``C'` là đường trung tuyến
giả sử: `BB'` cắt `C``C'` tại `G`
`-> G` là trọng tâm của Tam giác `ABC`
`-> GB = 2/3 BB'`
`-> GC = 2/3 C``C'`
`BB' = C``C' -> GB = GC`
`->` Tam giác `GBC` cân tại `G`
`->`\(\widehat{B_1}=\widehat{C_1}\)
Xét Tam giác `BB'C` và Tam giác `C``C'B` có:
`BB' = C``C'`
\(\widehat{B_1}=\widehat{C_1}\)
`BC` chung
`=>`Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`-> BC' = B'C`
`-> 1/2 AB = 1/2 AC`
`-> AB = AC`
`->` Tam giác `ABC` cân tại `A (đpcm)`.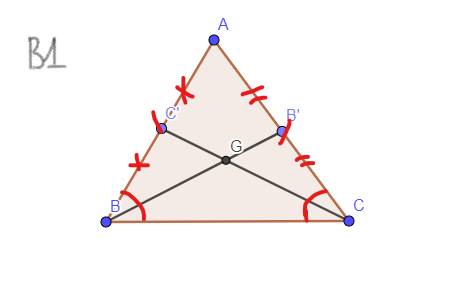

Hướng dẫn:

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF (giả thiết)
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=> \(\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được ba góc của chúng bằng nhau, suy ra đó là tam giác đều.
Bạn Thien Tu Borum làm nhanh vô rồi sai hình thức rồi kìa

A B C E D
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)

Vẽ BH⊥ACvà CK⊥AB
Xét hai tam giác vuông KBC và HCB có:
Cạnh BC chung
BH=CK(gt)
⇒ΔKBC=ΔHCB
⇒KBCˆ=HCBˆ
Xét tam giác ABC, có:
KBCˆ=HCBˆ hay ABCˆ=ACBˆ
Vậy tam giác ABC cân tại A (đpcm)
Ba đường cao bằng nhau
Từ a) ta có:
Nếu BH = CK thì ΔABC cân tại A => AB = AC (1)
Nếu AI = BH thì ΔABC cân tại C => CA = CB (2)
Từ (1) và (2) ta có: AB = BC = AC
Vậy ΔABC là tam giác đều.

Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
\(\Rightarrow\widehat{FBC}=\widehat{ECB}\)
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng
minh được đó là tam giác đều.