GIải phương trình sau:
x6 + x5+ x4 + x3 + x2+ x+1 =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)

1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)

Ta thấy x = 1 không phải nghiệm của phương trình nên nhân 2 vế của phương trình với x - 1 ta có:
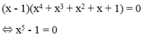
⇔ x = 1(KTM)
Vậy phương trình đã cho vô nghiệm.

x1;x2;x3;x4;x5=-1 hoặc 1
=>x1.x2;x2.x3;x3.x4;x4.x5;x5.x1 bằng 1 hoặc -1
giả sử x1.x2+x2.x3+x3.x4+x4.x5+x5.x1=0
=>số các số hạng 1 và -1 bằng nhau
=>số các số hạng chia hết cho 2
=>5 chia hết cho 2(có 5 số hạng) Vô lí
=>x1.x2+x2.x3+x3.x4+x4.x5+x5.x1\(\ne0\)
=>đpcm

ọi phương trình là A
A <=> 4x^6 + 4x^5 + 4x^4 + 4x^3 + 4x^2 + 4x + 3 + 1 = 0
<=> (4x^6 + 4x^5 + x^4) + (2x^4 + 4x^3 + 2x^2) + (2x^2 + 4x + 2) + x^4 + 2 = 0
<=> [2.(2x^3 + x^2)^2 + 2.(√2.x^2 + √2 . x)^2 + 2.(x+1)^2 + x^4] + 2 = 0
Xét tổng các số hạng trong ngoặc vuông, các số hạng đều có thừa số 2>0, thừa số còn lại là bình phương của 1 số sẽ > 0, còn số hạng ngoài ngoặc (số 2) hiển nhiên > 0. Từ đây suy ra phương trình A vô nghiệm.
Còn cách nữa chứng minh phương trình trên vô nghiệm. Nhân cả 2 vế với x-1 rồi thu gọn, ta có phương trình: x^7 - 1 = 0 <=> x = 1.
Ta thấy x = 1 không là nghiệm của phương trình A, vậy ta có phương trình A vô nghiệm.
(Bài tính thì theo bài của bạn, còn phần chứng minh năm ở bài 290, sách Nâng cao và phát triển toán 8 tập 2, trang 15)
P/S: Đình Huy ơi, chỗ (x + 1/x)^3 - 3.x.1/x.(x + 1/x) hình như phải là (x + 1/x)^3 - 3.x.1/x.(x - 1/x) chứ nhỉ?
cách đơn giản hơn nhé.
Đặt \(A=x^6+x^5+x^4+x^3+x^2+x+1=0\)
\(\Leftrightarrow\)\(x^5\left(x+1\right)+x^3\left(x+1\right)+x\left(x+1\right)+1=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x^5+x^3+x\right)+1=0\)
\(\Leftrightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)+1=0\)
Ta có: \(x^4+x^2+1=\left(x^2+\frac{1}{2}\right)+\frac{3}{4}>0\) \(\forall x\)
Nếu \(x\ge0\)thì \(x+1>0\)\(\Rightarrow\)\(x\left(x+1\right)\left(x^4+x^2+1\right)\ge0\)\(\Rightarrow\)\(A>1\)
Nếu \(x=-1\) thì \(x+1=0\)\(\Rightarrow\) \(A=1\)
Nếu \(x< -1\) thì \(x+1< 0\) \(\Rightarrow\) \(A>0\)
Vậy pt vô nghiệm
P/s: sai đâu m.n chỉ cho mk nhé