CMR : Pt \(\frac{1}{cosx}-\frac{1}{sinx}=m\) có nghiệm với mọi m thuộc R, sử dụng hàm số liên tục
giúp mik vsss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
AH
Akai Haruma
Giáo viên
4 tháng 3 2018
Lời giải:
Ta có: \(\frac{1}{\cos x}-\frac{1}{\sin x}=m\)
\(\Leftrightarrow f(x)=\frac{1}{\cos x}-\frac{1}{\sin x}-m=0\)
Ta thấy: Hàm \(f(x)\) liên tục trên đoạn \(\left[\frac{\pi}{6}; \frac{\pi}{3}\right]\), mà:
\(f\left(\frac{\pi}{3}\right)=\frac{6-2\sqrt{3}}{3}-m\)
\(f\left(\frac{\pi}{6}\right)=\frac{-6+2\sqrt{3}}{3}-m\)
\(\Rightarrow f\left(\frac{\pi}{3}\right)f\left(\frac{\pi}{6}\right)=\left(\frac{6-2\sqrt{3}}{3}-m\right)\left(\frac{-6+2\sqrt{3}}{3}-m\right)=-\left(\frac{6-2\sqrt{3}}{3}-m\right)^2\)
\(\Rightarrow f\left(\frac{\pi}{3}\right)f\left(\frac{\pi}{6}\right)\leq 0\)
Do đó tồn tại ít nhất một nghiệm \(c\in \left[\frac{\pi}{6}; \frac{\pi}{3}\right]\)
Ta có đpcm.
JE
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 9 2020
\(sinx-cosx=msinx+mcosx+m\)
\(\Leftrightarrow\left(m-1\right)sinx+\left(m+1\right)cosx=-m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(m-1\right)^2+\left(m+1\right)^2\ge\left(-m\right)^2\)
\(\Leftrightarrow m^2+2\ge0\) (luôn đúng)
Vậy pt có nghiệm với mọi m
CM
19 tháng 3 2019
Chọn D.
Phương pháp:
+ Đặt 3 sin x - cos x - 1 2 cos x - sin x + 4 = t biến đổi đưa về a sin x + b cos x = c , phương trình này có nghiệm khi a 2 + b 2 ≥ c 2 từ đó ta tìm ta được điều kiện của t.
+ Dựa vào đồ thị hàm số để xác định điều kiện nghiệm của phương trình f x = f t
Từ đó suy ra điều kiện có nghiệm của phương trình đã cho.
Chú ý rằng nếu hàm f t đồng biến (hoặc nghịch biến) trên (a;b) thì phương trình f u = f v nếu có nghiệm thì đó là nghiệm duy nhất trên a ; b ⇔ u = v
PA
0
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 10 2019
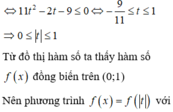
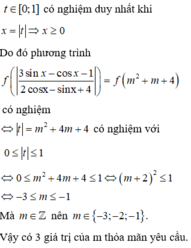
\(\Leftrightarrow m\left(sinx+cosx+1\right)=sin^2x+cos^2x+2sinx.cosx\)
\(\Leftrightarrow m\left(sinx+cosx+1\right)=\left(sinx+cosx\right)^2\)
Đặt \(sinx+cosx=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=t\)
\(x\in\left[0;\frac{\pi}{2}\right]\Rightarrow x+\frac{\pi}{4}\in\left[\frac{\pi}{4};\frac{3\pi}{4}\right]\Rightarrow t\in\left[1;\sqrt{2}\right]\)
Phương trình trở thành: \(t^2=m\left(t+1\right)\Leftrightarrow\frac{t^2}{t+1}=m\) (1)
\(f\left(t\right)=\frac{t^2}{t+1}\) đồng biến trên \(\left[1;\sqrt{2}\right]\Rightarrow f\left(1\right)\le f\left(t\right)\le f\left(\sqrt{2}\right)\)
\(\Leftrightarrow\frac{1}{2}\le f\left(t\right)\le2\sqrt{2}-2\)
\(\Rightarrow\frac{1}{2}\le m\le2\sqrt{2}-2\)