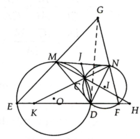
Cho 2 đường tròn (O) và (I) cắt nhau tại C và D,trong đó tiếp tuyến chung MN song song với cát tuyến EDF,M và N thuộc (O),N và F thuộc (I).D nằm giữa E và F.Gọi K,H theo thứ tự là giao điểm của NC,MC với EF.G là giao điểm của EM,FN.Chứng minh :
a) tam giác GMN và tam giác DMN bằng nhau
b) GD là trung trực của KH


Gọi đoạn thẳng MN thuộc tia xy ( xM<xN)
a, Xét đ.tr (O) có : góc xME là góc tạo bởi tt và dây cung chắc cung ME và MDE là góc nt chắn cung ME
=> góc xME=MDE. Vì MN//EF => góc MDE=NMD ( so le trong ).
Mà góc GMN=xME ( đối đỉnh ) => góc GMN=DMC (1)
Tương tự ta có : GNM=MND (2)
Xét tam giác GMN và DMN có :
(1) và (2)
Cạnh MN chung
=> tam giác DMN=DMN ( g.c.g )