Tìm các số x, y, z biết :
X+y = x:y=3(x-y)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 10 2021
\(2a=3b\Rightarrow\dfrac{a}{3}=\dfrac{b}{2}\Rightarrow\dfrac{a}{21}=\dfrac{b}{14}\\ 5b=7c\Rightarrow\dfrac{b}{7}=\dfrac{c}{5}\Rightarrow\dfrac{b}{14}=\dfrac{c}{10}\\ \Rightarrow\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}=\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}=\dfrac{3a-7b+5c}{63-98+50}=\dfrac{-30}{15}=-2\\ \Rightarrow\left\{{}\begin{matrix}a=-42\\b=-28\\c=-20\end{matrix}\right.\)
15 tháng 10 2021
\(x:y:z=3:4:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\Rightarrow x=3k;y=4k;z=5k\)
\(2x^2+2y^2-3z^2=-100\\ \Rightarrow18k^2+32k^2-75k^2=-100\\ \Rightarrow-25k^2=-100\Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=8;z=10\\x=-6;y=-8;z=-10\end{matrix}\right.\)
H
1
QS
2
25 tháng 12 2016
Giải:
Ta có:
x + y = 2
y + z = 3
z + x = -5
\(\Rightarrow x+y+y+z+z+x=2+3+\left(-5\right)\)
\(\Rightarrow2x+2y+2x=0\)
\(\Rightarrow2\left(x+y+z\right)=0\)
\(\Rightarrow x+y+z=0\)
\(\Rightarrow x=0-3=-3\)
\(\Rightarrow y=0-\left(-5\right)=5\)
\(\Rightarrow z=0-2=-2\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(-3;5;-2\right)\)
25 tháng 12 2016
ta có x + y = 2, y + z = 3, z + x = -5
=> x + y + y +z + z + x = 2 + 3 + -5
=> 2(x + y+ z) = 0
=>x + y + z = 0
mà x + y = 2 => z= -2
tương tự => x = -3 và y = 5
PT
1
CM
11 tháng 8 2018
Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
16 tháng 7 2015
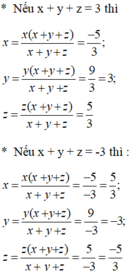
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
HN
2
27 tháng 6 2019
bạn tham khảo nè:
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
K2
0
HB
2
30 tháng 9 2016
Ta có:x/2=y/4=z/6 =x-y+z/2-4+6=x-y+z=8/2-4+6=4=8/4
Ta thấy:8/4=2/1=2
Vì thế x=2x2=4
y=2x4=8
z=2x6=12
Vậy đáp số là:x=4;y=8;z=12
Nhớ k cho mình nha !Cảm ơn nhiều
C
30 tháng 9 2016
Vì \(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}\)và x-y+z=8
Đặt \(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}=k\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=4k\\z=6k\end{cases}}\)
mà x+y+z=8 \(\Rightarrow\)2k-4k+6k=8
\(\Rightarrow\)4k=8
\(\Leftrightarrow\)k=2
Vậy \(\hept{\begin{cases}x=4\\y=8\\z=12\end{cases}}\)
x+y=x;y=3.[x-y]
x+y=x.\(\frac{1}{y}\)=3[x-y]
-x-y=x.\(\frac{1}{y}\)=3.[x-y]
=x.\(\frac{1}{y}\)=3[x-y]+x-y
=x\(\frac{1}{y}\)=4 .[x-y]
=1/yx=4x-4y
=1/yx-4x=4y
=1=4y
y=1/4
Có: \(x+y=3\left(x-y\right)\)\(x+y=3x-3y\)\(2x=4y\)\(\frac{x}{y}=2\)\(x=2y\)
Thay x = 2y vào x + y, ta được: \(3y=\frac{x}{y}\)
Có: \(\hept{\begin{cases}\frac{x}{y}=3y\\\frac{x}{y}=2\end{cases}\Rightarrow3y=2\Rightarrow y=\frac{2}{3}}\)
\(\Rightarrow x=2.\frac{2}{3}=\frac{4}{3}\)
Vậy \(x=\frac{4}{3};y=\frac{2}{3}\)