VP
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 7 2015
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
15 tháng 10 2021
\(2a=3b\Rightarrow\dfrac{a}{3}=\dfrac{b}{2}\Rightarrow\dfrac{a}{21}=\dfrac{b}{14}\\ 5b=7c\Rightarrow\dfrac{b}{7}=\dfrac{c}{5}\Rightarrow\dfrac{b}{14}=\dfrac{c}{10}\\ \Rightarrow\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}=\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}=\dfrac{3a-7b+5c}{63-98+50}=\dfrac{-30}{15}=-2\\ \Rightarrow\left\{{}\begin{matrix}a=-42\\b=-28\\c=-20\end{matrix}\right.\)
15 tháng 10 2021
\(x:y:z=3:4:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\Rightarrow x=3k;y=4k;z=5k\)
\(2x^2+2y^2-3z^2=-100\\ \Rightarrow18k^2+32k^2-75k^2=-100\\ \Rightarrow-25k^2=-100\Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=8;z=10\\x=-6;y=-8;z=-10\end{matrix}\right.\)
30 tháng 9 2016
Ta có:x/2=y/4=z/6 =x-y+z/2-4+6=x-y+z=8/2-4+6=4=8/4
Ta thấy:8/4=2/1=2
Vì thế x=2x2=4
y=2x4=8
z=2x6=12
Vậy đáp số là:x=4;y=8;z=12
Nhớ k cho mình nha !Cảm ơn nhiều
C
30 tháng 9 2016
Vì \(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}\)và x-y+z=8
Đặt \(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}=k\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=4k\\z=6k\end{cases}}\)
mà x+y+z=8 \(\Rightarrow\)2k-4k+6k=8
\(\Rightarrow\)4k=8
\(\Leftrightarrow\)k=2
Vậy \(\hept{\begin{cases}x=4\\y=8\\z=12\end{cases}}\)
PT
1
CM
11 tháng 8 2018
Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
K
2
27 tháng 7 2018
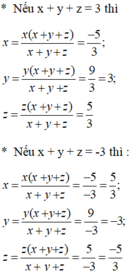
Vì xy = x : y suy ra y^2 = 1 ---> y = 1 hoặc y = -1
+ Nếu y = 1 ---> x - 1 = x.1 (vô nghiệm nên tr/hợp này loại)
+ Nếu y = -1 ---> x + 1 = - x ---> 2x = -1 ---> x = -1/2 (nhận)
Vậy x = -1/2 ; y = -1.
28 tháng 7 2018
l.anh êi , mở bài 21 trang 11 trong vở bài tập có bài này đấy
PH
0
S
2
MN
22 tháng 2 2016
Ta có: (3x-5)2006 lớn hơn hoặc = 0 với mọi x
(y2-1)2008 lớn hơn hoặc = 0 vs moi y
(x-z)2100 lớn hơn hoặc = 0 vs mọi x, z
=> (3x-5)2006+(y2-1)2008+(x-z)2100 lớn hơn howacj = 0 vs mọi x
mà (3x-5)2006+(y2-1)2008+(x-z)2100=0
=> (3x-5)2006=0 ; (y2-1)2008=0 và (x-z)2100=0
+) xét (3x-5)2006=0
=>3x-5=0
=>3x=5
=>x=5/3
+) xét (y2-1)2008=0
=>y2-1=0
=>y2=1
=>y=-1 hoặc y=1
+) xét (x-z)2100=0
=>x-z=0
=>5/3-z=0
=>z=5/3
BH
0
x+y=x;y=3.[x-y]
x+y=x.\(\frac{1}{y}\)=3[x-y]
-x-y=x.\(\frac{1}{y}\)=3.[x-y]
=x.\(\frac{1}{y}\)=3[x-y]+x-y
=x\(\frac{1}{y}\)=4 .[x-y]
=1/yx=4x-4y
=1/yx-4x=4y
=1=4y
y=1/4
Có: \(x+y=3\left(x-y\right)\)\(x+y=3x-3y\)\(2x=4y\)\(\frac{x}{y}=2\)\(x=2y\)
Thay x = 2y vào x + y, ta được: \(3y=\frac{x}{y}\)
Có: \(\hept{\begin{cases}\frac{x}{y}=3y\\\frac{x}{y}=2\end{cases}\Rightarrow3y=2\Rightarrow y=\frac{2}{3}}\)
\(\Rightarrow x=2.\frac{2}{3}=\frac{4}{3}\)
Vậy \(x=\frac{4}{3};y=\frac{2}{3}\)