Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
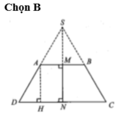
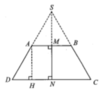
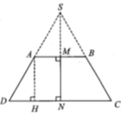
Gọi S là giao điểm của AD và BC. Nếu quay tam giác SCD quanh trục SN, các đoạn thẳng SC. SB lần lượt tạo ra mặt xung quanh của hình nón ( H 1 ) v à ( H 2 ) .
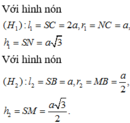
Do ABCD là hình thang cân
\(\Rightarrow AD=BC\) và \(\widehat{FDA}=\widehat{FCB}\)
Do F là trung điểm của CD (gt)
\(\Rightarrow FC=FD\)
Xét \(\Delta ADF\) và \(\Delta BCF\) có:
\(AD=BC\) (cmt)
\(\widehat{FDA}=\widehat{FCB}\) (cmt)
\(FD=FC\) (cmt)
\(\Rightarrow\Delta ADF=\Delta BCF\) (c-g-c)
\(\Rightarrow AF=BF\) (hai cạnh tương ứng)
\(\Delta FAB\) có:
\(AF=BF\) (cmt)
\(\Rightarrow\Delta FAB\) cân tại F
Lại có E là trung điểm của AB
\(\Rightarrow FE\) là đường trung tuyến của \(\Delta FAB\)
\(\Rightarrow FE\) cũng là đường cao của \(\Delta FAB\)
\(\Rightarrow FE\perp AB\)
Mà AB // CD (gt)
\(\Rightarrow FE\perp CD\)
Vậy EF vuông góc với AB và CD
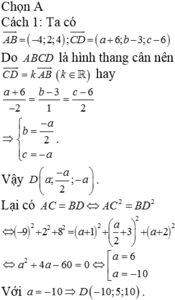
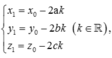
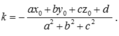
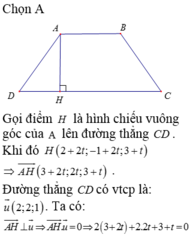
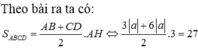
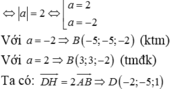
Chọn A
Cách 1: Ta có
Do ABCD là hình thang cân nên
Lại có AC = BD
Với a = -10 => D(-10;5;10). Kiểm tra thấy: A B → = C D → (Không thỏa mãn ABCD là hình thang cân).
Với a= 6 => D(6; -3; -6). Kiểm tra thấy: 3. A B → = C D → ( thỏa mãn).
Do đó
Cách 2
Ta có
Do ABCD là hình thang cân nên A B → ; C D → ngược hướng hay
Lại có AB = CD
Do đó
Cách 3
+ Viết phương trình mặt phẳng trung trực của đoạn thẳng AB( cũng là mp trung trực của đoạn thẳng CD )
+ Gọi mp α là mặt phẳng trung trực của đoạn thẳng AB, suy ra mp α đi qua trung điểm I(1;2;0) của đoạn thẳng AB và có một vectơ pháp tuyến là
suy ra phương trình của mp α là :
+ Vì C, D đối xứng nhau qua mp α nên
Công thức trắc nghiệm
Xác định toạ độ điểm M ' ( x 1 ; y 1 ; z 1 ) là điểm đối xứng của điểm M ( x 0 ; y 0 ; z 0 ) qua mp