Bài 1: Cho (O;R) và điểm A nằm ngoài (O) sao cho OA=3R. Từ A vẽ 2 tiếp tuyến AB; AC với (O)
a) CMR: Tứ giác OBAC nội tiếp
b) CMR: OA ⊥ BC
c) Từ B vẽ đường thẳng // AC cắt (O) tại D; AD cắt (O) tại E. Tính AD.AE theo R
d) Tia BE cắt AC tại F. CMR: F là trung điểm AC
Bài 2: Cho ΔABC nhọn nội tiếp (O); hai điểm B;C cố định. Điểm A di chuyển trên cung lớn BC. Gọi H là hình chiếu của A xuống BC. Gọi M;N lần lượt là hình chiếu của B;C đến đường kính AD
a) C/m các điểm A;B;H;M cùng thuộc một đường tròn
b) C/m ΔHMN ∽ ΔABC
c) Gọi I;E lần lượt là trung điểm BC và AB. C/m IE là trung trực của HM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
a: Độ dài cung nhỏ AB là:
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=\dfrac{pi\cdot R\cdot2}{3}\)
Độ dài cung nhỏ BC là;
\(\dfrac{2\cdot pi\cdot R\cdot120}{360}=pi\cdot R\cdot\dfrac{2}{3}\)
b: \(S=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
c: Diện tích hình quạt tròn OAC là:
\(S_q=\dfrac{pi\cdot R^2\cdot120}{360}=pi\cdot\dfrac{R^2}{3}\)
Diện tích tam giác OAC là:
\(S=\dfrac{1}{2}\cdot OA\cdot OC\cdot sin120=\dfrac{1}{4}\cdot R^2\)
Diện tích hình viên phân OAC là;
\(S_q-S=R^2\left(\dfrac{pi}{3}-\dfrac{1}{4}\right)\)

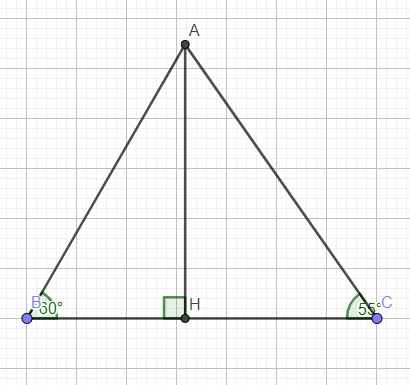
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)