Cho AB và CD là hai đường kính vuông góc của(O;R). Trên tia đối của CO lấy điểm S. SA cắt (O) tại M. Tiếp tuyến tại M với (O) cắt CD tại E, BM cắt CD tại F. a) c/m EA. AM=MF.OAb) SB cắt (O) tại I. c/m A,I,F thẳng hàngc) Giả sử EM=R. Tính FA.SM theo Rd) kẻ MH vuông góc với AB tại H. xác định vị trí điểm S để diện tích tam giác MHD lớn...
Đọc tiếp
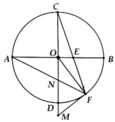
Cho AB và CD là hai đường kính vuông góc của(O;R). Trên tia đối của CO lấy điểm S. SA cắt (O) tại M. Tiếp tuyến tại M với (O) cắt CD tại E, BM cắt CD tại F. a) c/m EA. AM=MF.OA
b) SB cắt (O) tại I. c/m A,I,F thẳng hàng
c) Giả sử EM=R. Tính FA.SM theo R
d) kẻ MH vuông góc với AB tại H. xác định vị trí điểm S để diện tích tam giác MHD lớn nhất
a: Sửa đề: \(EM\cdot AM=MF\cdot OA\)
\(\widehat{EMO}=\widehat{EMF}+\widehat{OMF}\)
=>\(\widehat{EMF}+\widehat{OMF}=90^0\)(1)
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMO}+\widehat{FMO}=\widehat{AMF}=90^0\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{EMF}=\widehat{AMO}\)
=>\(\widehat{EMF}=\widehat{OAM}\)
ΔMEO vuông tại M
=>\(\widehat{MEO}+\widehat{MOE}=90^0\)
=>\(\widehat{MEF}+\widehat{MOE}=90^0\)(3)
Ta có: OM nằm giữa OA và OE
=>\(\widehat{AOM}+\widehat{MOE}=90^0\)(4)
từ (3) và (4) suy ra \(\widehat{MEF}=\widehat{AOM}\)
Xét ΔMEF và ΔAOM có
\(\widehat{MEF}=\widehat{AOM}\)
\(\widehat{EMF}=\widehat{OAM}\)
Do đó: ΔMEF đồng dạng với ΔAOM
=>ME/AO=MF/AM
=>\(ME\cdot AM=AO\cdot MF\)
b: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
Do đó: ΔAIB vuông tại I
=>AI\(\perp\)SB
Xét ΔSAB có
BM,SO là đường cao
BM cắt SO tại F
Do đó; F là trực tâm
=>AF\(\perp\)SB
mà AI\(\perp\)SB(cmt)
và AF,AI có điểm chung là A
nên A,I,F thẳng hàng