cho đường thẳng d là đường trung trực AB . M;N thuộc d . chứng minh tam giác AMN = tam giác BMN bằng 3 cách (g.c.g ; c.c.c; c.g.c)
Giúp mk với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2018
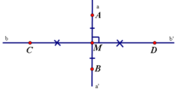
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
17 tháng 9 2023
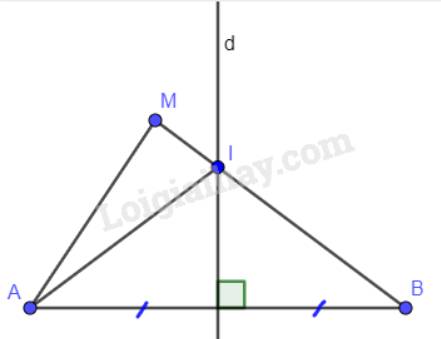
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).
LV
31 tháng 10 2021
a, kẻ đoạn AB bằng thước 4cm
gọi I là trung điểm AB , từ I kẻ đường thẳng d vuông góc vs AB , ta dc d là đường trung trực của AB
b, gọi M là điểm thuộc d , VẼ
c, Vì ta có AB vuông góc vs d mà a song song vs AB
suy ra a vuông góc vs đường thẳng d
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5
d M N A B
Gọi O là giao điểm của AB và d
Vì d là đường trung trực (đtt ) của AB => Tam giác AOM = tam giác BOM ( c.g.c )
=> Tam giác AON = tam giác BOM ( c.g.c )
=> AM = BM và AN = BN, g AMN = g BMN, g ANO = g BNO hay g ANM = g BNM
Từ những điều kiện trên ta suy ra:
=> tam giác AMN = tam giác BMN ( c.c.c )
=> tam giác AMN = tam giác BMN ( c.g.c )
=> tam giác AMN = tam giác BMN ( g.c.g )
( Đây là lời giải tóm tắt của mik, bạn nhớ giải đầy đủ ra nhé )