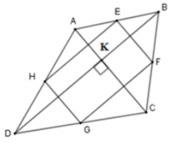
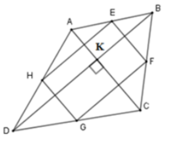
Cho tứ giác ABCD. Gọi E,F,G,H là trung điểm của bốn cạnh AB,BC,CD,DA; M,N là trung điểm hai đường chéo BD và AC. O là trung điểm của EG. Chứng minh: véc tơ AB + véc tơ AC + véc tơ AD = 4 . vecto AO
mọi người ơi giúp em với, bạn nào giúp mình sẽ gửi 1 card điện thoại 50k thay lời cám ơn ạ.