Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

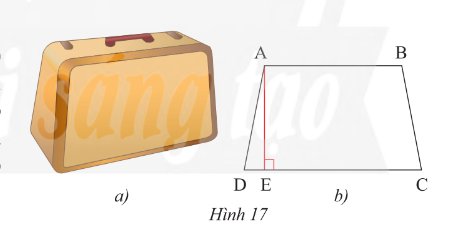
Áp dụng định lý Pythagore vào tam giác vuông \(ADE\) ta có:
\(D{E^2} + A{E^2} = A{D^2}\)
\(D{E^2} = A{D^2} - A{E^2} = {61^2} - {60^2} = 121 = {11^2}\)
\(DE = 11\) (cm)
Độ dài \(AB\) là: \(92 - 11.2 = 70\) (cm)

Bài 1:
\(S=\dfrac{12+20}{2}\cdot8=16\cdot8=128\left(cm^2\right)\)
Bài 2:
Vì ABCD là hình thang cân (gt)
Suy ra: BD = AC (hình thang cân có hai đường chéo bằng nhau)
BD = 5cm (gt)
AC = 3cm (gt)
5cm > 3cm
Suy ra BD > AC (vô lí)
Vậy không tồn tại hình thang cân nào thỏa mãn đề bài.

a) Cách 1:Kéo dài các cạnh bên, cắt nhau tại E, dể dàng thấy tg ECD cân tại E, mà CD = 2AB và AB//CD => AB là đường trung bình => A, B lần lượt là trung điểm của DE và CE => CD = CE = DE => tgDEC đều => ^ADB = 60. => các góc còn lại.
Cách 2: Từ A kẻ AE//BC => ABCE là hình bình hành =>AE = BC = DC/2 = DE => AE = DE = AD => tgADE đều => ^ADE = 60độ.
b) AH = 4 căn 3 => AD^2 = AH^2 + DH^2 = AH^2 + (AD/2)^2
= AH^2 + AD^2/4 => 3AD^2 = 4AH^2 = 4.14.3
=> AD=8 => chu vi = 5AD =40.

Góc ACD vuông, góc D=60 độ thì CAD=30 độ và tam giác ACD là nửa tam giác đều, hay AD=2CD.
Góc BAC=CAD=30 độ thì BAD= 60 độ, hình thang này cân, và AB=CD
Góc BCD bù góc D nên BCD=120 độ, vậy BCA=30 độ. Tam giác ABC cân, hay AB=BC.
Tóm lại chu vi hình thang = 5 CD=2,5 AD.
AD=20/2,5=8cm