CHO \(\Delta ABC\)VUÔNG TẠI A, ĐƯỜNG CAO AH. KẺ \(HD\perp AB;HE\perp AC\)
A) CHỨNG MINH \(AD.AB=AE.AC\)
B) CHỨNG MINH \(DE^3=BC.BD.CE\)
GIÚP MÌNH VỚI!!!!!!!!!!!!!!!!CÁM ƠN NHIỀU!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,
xét \(\Delta\) AHD và \(\Delta\) AHB có
<DAH chung
< ADH=<AHB(=90)
\(\Rightarrow\Delta AHD\) ~ \(\Delta AHB\)
b,\(\dfrac{\Rightarrow AH}{BA}=\dfrac{AD}{AH}\Rightarrow AH^2=AB\cdot AD\)
ta có <ABC+< BAH=90\(^0\)
< BAH+<HAC=90\(^0\)
\(\Rightarrow\) <ABC=<HAC
xét \(\Delta\) ABH và \(\Delta\) CAH
<ABH=<CAH (cmt)
<AHB=<AHC(=90)
\(\Rightarrow\Delta ABH\) ~ \(\Delta CAH\)
\(\dfrac{\Rightarrow AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=HB\cdot HC\)
ta có \(AB\cdot AD=AH^2\)
\(HB\cdot HC=AH^2\)
\(\Rightarrow AD\cdot AB=HB\cdot HC\) (dpcm)
Hình tự vẽ nha
a) Xét Δ AHD và Δ AB có
∠ H = ∠ D ( = 90o )
∠ A chung
Vậy △ AHD ∼ △ADB

bn tham khảo ở đây nha:http://text.123doc.org/document/658748-6-bai-toan-hinh-4-de-thi-ki-i-toan-8.htm

Chứng minh:
a) Vì △ABC cân tại A ⇒ AB = AC
Xét △ABH và △ACH có:
AB = AC (cmt)
\(\widehat{BAH}=\widehat{CAH}\) (gt)
AH - cạnh chung
⇒△ABH = △ACH (c.g.c)
⇒ ( tương ứng)
⇒ HB = HC ( tương ứng)
Vì \(\widehat{AHB}+\widehat{AHC}=180^o\) ( kề bù)
mà \(\widehat{AHB}=\widehat{AHC}\) (cmt)
⇒ \(\widehat{AHB}=\widehat{AHC}=90^o\)
⇒ AH ⊥ BC ⇒ AH là đường cao của △ABC
b)
Xét △AHD vuông tại D và △AHE vuông tại E có:
\(\widehat{DAH}=\widehat{EAH}\text{ (gt)}\)
AH - cạnh chung
⇒ △AHD = △AHE ( cạnh huyền - góc nhọn )
⇒ HD = HE ( tương ứng )

a/ Xét \(\Delta ABC\) và \(\Delta HAC\) có :
\(\left\{{}\begin{matrix}\widehat{C}chung\\\widehat{BAC}=\widehat{AHC}=90^0\end{matrix}\right.\)
\(\Leftrightarrow\Delta ABC\sim HAC\left(g-g\right)\)
b/ \(BC=\sqrt{AB^2+AC^2}=10cm\)
\(AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=4,8cm\)
c/ \(\Delta HEA\sim\Delta CEH\left(g-g\right)\)
\(\Leftrightarrow\dfrac{HE}{CE}=\dfrac{EA}{HE}\Leftrightarrow HE^2=EA.EC\left(đpcm\right)\)

a) Xét ΔHAC và ΔABC có:
∠(ACH ) là góc chung
∠(BAC)= ∠(AHC) = 90o
⇒ ΔHAC ∼ ΔABC (g.g)
b) Xét ΔHAD và ΔBAH có:
∠(DAH ) là góc chung
∠(ADH) = ∠(AHB) = 90o
⇒ ΔHAD ∼ ΔBAH (g.g)

c) Tứ giác ADHE có 3 góc vuông ⇒ ADHE là hình chữ nhật.
⇒ ΔADH= ΔAEH ( c.c.c) ⇒ ∠(DHA)= ∠(DEA)
Mặt khác: ΔHAD ∼ ΔBAH ⇒ ∠(DHA)= ∠(BAH)
∠(DEA)= ∠(BAH)
Xét ΔEAD và ΔBAC có:
∠(DEA)= ∠(BAH)
∠(DAE ) là góc chung
ΔEAD ∼ ΔBAC (g.g)

d) ΔEAD ∼ ΔBAC

ΔABC vuông tại A, theo định lí Pytago:

Theo b, ta có:
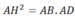



a) Xét ΔAHB vuông tại H và ΔADH vuông tại D có
\(\widehat{DAH}\) chung
Do đó: ΔAHB\(\sim\)ΔADH(g-g)

a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{HAB}=\widehat{BAC}=90^0\)
\(\widehat{B}:chung\)
do đó \(\Delta HBA\sim\Delta ABC\left(g-g\right)\)
b) Xét \(\text{ΔHBAvàΔHAC}\) có:
\(\widehat{BHA}=\widehat{CHA}=90^o\)
\(\widehat{ABH}=\widehat{HAC}\) ( do cùng phụ với \(\widehat{BAH}\))
Do đó: \(\Delta HBA\sim\Delta HAC\left(g-g\right)\)
\(\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow HA^2=HB\cdot HC\)
c) Xét tứ giác ADHE có:
\(\widehat{A}=\widehat{D}=\widehat{E}=90^o\)
Do đó ADHE là hình chữ nhật
Gọi O là giao điểm 2 đường chéo hình chữ nhật(AH và DE)
\(\Rightarrow OD=OA\)(tính chất HCN)
\(\Rightarrow\Delta ODA\) cân tại O
\(\Rightarrow\widehat{ODA}=\widehat{OAD}\)
Xét \(\Delta ADE\) và \(\Delta HAB\) có:
\(\widehat{BHA}=\widehat{DAE}=90^o\\ \widehat{ODA}=\widehat{OAD}\left(cmt\right)\\ \Rightarrow\Delta ADE\sim\Delta HAB\)
Mà \(\Delta HBA\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\) (tính chất bắc cầu)