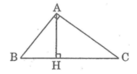
Bài 1 Vẽ tam giác ABC vuông tại A,đường cao AH.Hãy tính BC,AH,BH,CH trong các trường hợp sau
1/ BH=2cm;CH=8cm
2/BH=2cm;CH=2cm
3/BH=√5cm;CH=4√5cm
Ai giúp em với ạ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 6 2023
a: AH=căn 13^2-5^2=12cm
CH=12^2/5=28,8cm
BC=28,8+5=33,8cm
AC=căn 28,8*33,8=31,2cm
b: AH=căn 3*4=2căn 3(cm)
AB=căn 3*7=căn 21(cm)
AC=căn 4*7=2căn 7(cm)
c: CH=4^2/3=16/3cm
AB=căn 4^2+3^2=5cm
AC=căn 16/3*25/3=20/3(cm)
24 tháng 7 2018
a) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow16^2+25^2=AB^2\)
\(\Leftrightarrow AB=\sqrt{881}\left(cm\right)\)
Áp dụng hệ thức về đường cao trong tam giác vuông ta có :
\(AH^2=HB\times HC\)
\(\Leftrightarrow16^2=25\times HC\)
\(\Leftrightarrow HC=10,24\left(cm\right)\)
Ta có : \(BC=CH+BH=10,24+25=35,24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=35,24^2-\sqrt{881}^2\)
\(\Leftrightarrow AC=360,8576\left(cm\right)\)
b) Áp dụng Pi-ta-go cho \(\Delta AHB\)vuông tại H ta có :
\(AH^2=AB^2-HB^2\)
\(\Leftrightarrow AH^2=12^2-6^2\)
\(\Leftrightarrow AH=6\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức trong tam giác ta có :
\(AH^2=CH\times HB\)
\(\Leftrightarrow CH=18\left(cm\right)\)
Ta có : \(BC=CH+BH=18+6=24\left(cm\right)\)
Áp dụng Pi-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=24^2-12^2\)
\(\Leftrightarrow AC=12\sqrt{3}\left(cm\right)\)
Vậy ...
L
25 tháng 11 2020
a)
- Áp dụng định lí Py - ta - go cho tam giác vuông HAB ( \(\widehat{H}=90^o\))
\(AB^2=BH^2+AH^2\)
\(=25^2+16^2\)
\(=625+256=881\)
\(\Rightarrow AB=\sqrt{881}\approx29,6\left(cm\right)\)
- Áp dụng hệ thức lượng trong tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
+) AH2 = HB . HC
\(16^2=25.HC\)
\(HC=\frac{16^2}{25}=\frac{256}{25}=10,24\left(cm\right)\)
+) BC = BH + HC = 25 + 10,24 = 35,24 ( cm )
\(+)AC^2=HC.BC=10,24.35,24\approx360,86\left(cm\right)\)
\(\Rightarrow AC=\sqrt{360,86}\approx18,9cm\)
Vậy : ..................
b)
- Áp dụng định lí Py - ta - go cho tam giác vuông AHB ( \(\widehat{H}=90^o\)) , ta có :
AB2 = BH2 + AH2
122 = 62 + AH2
AH2 = 122 - 62
= 144 - 366 = 108 ( cm )
\(\Rightarrow AH=\sqrt{108}\approx10,39\left(cm\right)\)
- Áp dụng hệ thức lượng cho tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
\(+)AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{10,39^2}{6}=17,99\left(cm\right)\)
\(+)BC=BH+HC=6+17,99=23,99\left(cm\right)\)
\(+)AC^2=BC.HC=23,99.17,99=431,58\left(cm\right)\)
\(+)AC=\sqrt{431,58}\approx20,77\left(cm\right)\)
Vậy : ....................
NV
18 tháng 7 2018
27/12/2017 lúc 18:59
Ex1: Điền từ thích hợp vào chỗ trống
This is Ba. He(1)......... a student.Every morning he(2).........up at 5.30.He(3).............. his teeth and takes a(4)............... then has breakfast at 6.15. He goes to school(5)........six thirty.His house is(6).............his house so he walks.The classes(7)............at 7.15 and finish at 11.15.In the afternoon he plays sports with his friend,Nam. They play badminton but now they(8).................soccer.In the evening he (9)......his homework and goes to(10).........at 9.30
Ex2:Cho dạng đúng của động từ trong ngoặc
1.My sister(have)...........classes from Monday to Friday
2.She(read)................a book in her room now
3.He(get)........................up at 6.00 every day?
4.There(not be)..............a big yard behind his classroom
27/12/2017 lúc 18:59
Ex1: Điền từ thích hợp vào chỗ trống
This is Ba. He(1)......... a student.Every morning he(2).........up at 5.30.He(3).............. his teeth and takes a(4)............... then has breakfast at 6.15. He goes to school(5)........six thirty.His house is(6).............his house so he walks.The classes(7)............at 7.15 and finish at 11.15.In the afternoon he plays sports with his friend,Nam. They play badminton but now they(8).................soccer.In the evening he (9)......his homework and goes to(10).........at 9.30
Ex2:Cho dạng đúng của động từ trong ngoặc
1.My sister(have)...........classes from Monday to Friday
2.She(read)................a book in her room now
3.He(get)........................up at 6.00 every day?
4.There(not be)..............a big yard behind his classroom
27/12/2017 lúc 18:59
Ex1: Điền từ thích hợp vào chỗ trống
This is Ba. He(1)......... a student.Every morning he(2).........up at 5.30.He(3).............. his teeth and takes a(4)............... then has breakfast at 6.15. He goes to school(5)........six thirty.His house is(6).............his house so he walks.The classes(7)............at 7.15 and finish at 11.15.In the afternoon he plays sports with his friend,Nam. They play badminton but now they(8).................soccer.In the evening he (9)......his homework and goes to(10).........at 9.30
Ex2:Cho dạng đúng của động từ trong ngoặc
1.My sister(have)...........classes from Monday to Friday
2.She(read)................a book in her room now
3.He(get)........................up at 6.00 every day?
4.There(not be)..............a big yard behind his classroom
Dễ quá đi
8 tháng 1 2021
a. - Áp dụng hệ thức về cạnh và đường cao trong Δ vuông vào ΔABC vuông tại A ta có :
\(AH=\sqrt{CH.BH}=\sqrt{2.4}=2\sqrt{2}\) ( Đ.lý 2 )
- Áp dụng đ.lý Pytago vào \(\Delta AHB\perp H\) ta có :
\(AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{2}\right)^2+4^2}=2\sqrt{6}\)
- \(BC=2+4=6\)
- Theo đ.lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{6^2-\left(2\sqrt{6}\right)^2}=2\sqrt{3}\)
b. - Áp dụng hệ thức...trong Δ vuông ABC ta có :
+ \(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=24\) ( Đ.lý 1 )
\(\Rightarrow CH=BC-BH=24-6=18\)
+ \(AH=\sqrt{BH.CH}=\sqrt{6.18}=6\sqrt{3}\) ( Đ.'ý 2 )
- Theo đ.lý Pytago ta có :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{24^2-12^2}=12\sqrt{3}\)
8 tháng 1 2021
a, BC = BH+HC
*\(AB=\sqrt{BH.BC}=\sqrt{4.8}=\sqrt{32}\)
*\(AC=\sqrt{HC.BC}=\sqrt{2.8}=4\)
*\(AH=\sqrt{BH.HC}=\sqrt{4.2}=\sqrt{8}\)
b,Theo định lý pytago ta có:
\(AH=\sqrt{AB^2-BH^2}=\sqrt{12^2-6^2}=6\sqrt{3}\)
*\(BC=\dfrac{AB^2}{BH}=\dfrac{12^2}{6}=2\)
*\(CH=BC-BH=24-6=18\)
\(AC=\sqrt{HC.BC}=\sqrt{18.24}=12\sqrt{3}\)
CM
3 tháng 10 2018
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: A H 2 = B H . C H
⇒ CH =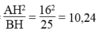 
BC = BH + CH = 25 + 10,24 = 35,24
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ AB = 
≈ 29,68
A C 2 = H C . B C
⇒ AC = 
≈ 18,99
CM
29 tháng 6 2017
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A
B
2
=
B
H
.
B
C
⇒ BC = 
= 24
CH = BC – BH = 24 – 6 = 18
Theo hệ thức liên hệ giữa các cạnh góc vuông và hình chiếu, ta có:
A
C
2
=
H
C
.
B
C
⇒ AC = 
≈ 20,78
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
A
H
2
=
H
B
.
B
C
⇒ AH = 
20 tháng 7 2017
a) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
AB2 = 152 + 252
AB2 = 225 + 625
AB2 = 850
AB = \(\sqrt{850}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
850 = 25.BC
BC = 850:25
BC = 34
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2
342 = 850 + AC2
1156 - 850 = AC2
AC2 = 306
AC = \(\sqrt{306}\)(cm)
Ta có BC = BH + HC
34 = 25 + HC
HC = 34 - 25
HC = 9
b) Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (ĐL Py-ta-go)
122 = AH2 + 62
144 = AH2 + 36
AH2 = 144 - 36
AH2 = 108
AH = \(\sqrt{108}\)(cm)
Xét tam giác ABC vuông tại A, có đường cao AH:
=> BA2 = BH.BC
122 = 6.BC
144 = 6.BC
BC = 144:6
BC = 24 (cm)
Ta có BC = BH + HC
24 = 6 + HC
HC = 24 - 6
HC = 18
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 (ĐL Py-ta-go)
242 = 122 + AC2
AC2 = 242 - 122
AC2 = 576 - 144
AC2 = 432
AC = \(\sqrt{432}\)(cm)
12 tháng 5 2018
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB = \(\sqrt{881}\)
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC = \(\sqrt{\text{360,8576}}\)
3 tháng 9 2020
Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
HC
3 tháng 9 2020
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
Bn tự vẽ hình nha:)
Mà đề cho BH,CH rồi thì tính toán rì nữa-.-?
1) Ta có: \(\hept{\begin{cases}AH^2=BH.CH=2.8=16\\BC=BH+CH=2+8\end{cases}}\Rightarrow\hept{\begin{cases}AH=4\left(cm\right)\\BC=10\left(cm\right)\end{cases}}\)
2) Ta có: \(\hept{\begin{cases}AH^2=BH.CH=2.2=4\\BC=BH+CH=2+2\end{cases}}\Rightarrow\hept{\begin{cases}AH=2\left(cm\right)\\BC=4\left(cm\right)\end{cases}}\)
3) Ta có: \(\hept{\begin{cases}AH^2=BH.CH=\sqrt{5}.4\sqrt{5}=\left(2\sqrt{5}\right)^2\\BC=BH+CH=\sqrt{5}+4\sqrt{5}\end{cases}}\Rightarrow\hept{\begin{cases}AH=2\sqrt{5}\left(cm\right)\\BC=5\sqrt{5}\left(cm\right)\end{cases}}\)
Nếu đề bắt tính cả AB,AC thì ib mk làm lại cho:)