3x = y; 5y = 4z và 6x + 7y + 8z = 456
(Tìm x, y, z)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
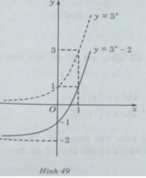
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
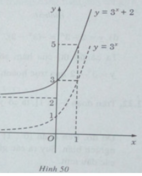
c) 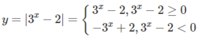
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
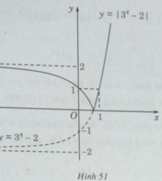
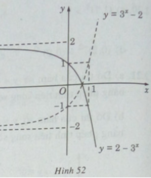
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).

\(=\dfrac{3x-y+6x+4y}{3x+y}=\dfrac{9x+3y}{3x+y}=\dfrac{3\left(3x+y\right)}{3x+y}=3\)

PT của đường thẳng cần tìm có dạng: `(d): y=ax+b `
`(d)` vuông góc `(d') : y=1/3 x-7/3 <=> a. 1/3 = -1 <=> a=-3`
`=> y=-3x+b`
`A (0;4) \in (d) <=> 4=-3.0+b <=> b=4`
`=> y=-3a+4`.

Lời giải:
Màu xanh lá: $y=3x$
Màu xanh nước biển: $y=-3x$
Màu đỏ: $y=\frac{x}{2}$
Màu cam: $y=\frac{-x}{3}$


Lời giải:Đồ thị xanh lá là $y=3x$
Đồ thị xanh dương là $y=-3x$
Đồ thị hồng là $y=\frac{1}{2}x$
Đồ thị cam là $y=-\frac{1}{3}x$
Cách vẽ đồ thị là bạn lấy 2 điểm thuộc đồ thị rồi nối với nhau. Ví dụ như đồ thị $y=-3x$ ta nối 2 điểm $(0;0)$ và $(1;-3)$

a) y = 3x
Cho x = 1 \(\Rightarrow\) y = 3 \(\Rightarrow\) A(1; 3)
Đồ thị:


Đặt \(t=3x+y\)
pt \(\Leftrightarrow t^3-3t^2+3t-1=-27\)
\(\Leftrightarrow\left(t-1\right)^3+3^3=0\)
\(\Leftrightarrow\left(t-1+3\right)\left(\left(t-1\right)^2-3\left(t-1\right)+9\right)=0\)
\(\Leftrightarrow\left(t+2\right)\left(t^2-5t+13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t+2=0\\t^2-5t+13=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-2\\t^2-5t+13=0\left(vl\right)\end{matrix}\right.\)
\(\Leftrightarrow3x+y=-2\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2-3x\\x\in R\end{matrix}\right.\)
\(\Rightarrow\frac{x}{1}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x}{4}=\frac{y}{12}=\frac{z}{15}=\frac{6x+7y+8z}{6.4+7.12+8.15}=\frac{456}{228}=2\)
=> x= 4.2 =8
y = 12.2 =24
z = 15.2 =30