Giúp em ạ:
Cho các số thực a, b, c thuộc đoạn [1;3] sao cho a+b+c=6. Chứng minh rằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\left|a\right|\le1;\left|b-1\right|\le2\)
\(=>\left|a\right|\cdot\left|b-1\right|=\left|ab-a\right|\le2\)
Áp dụng BĐT \(\left|x\right|+\left|y\right|\ge\left|x+y\right|\) ta có:
\(\left|a-c+ab-a\right|\le\left|a-c\right|+\left|ab-a\right|=2+3=5\)
\(=>\left|ab-c\right|\le5\)

a) a = 2
+ y = f(1) = 2.1 = 2
+ y = f(-2) = 2.(-2) = -4
+ y = f(-4) = 2.(-4) = -8
b) f(2) = 4
=> 4 = a.2
=> a = 2
( Vẽ đồ thị hàm số thì bạn tự vẽ được mà :)) Ở đây vẽ hơi khó )
c) Khi a = 2
=> Ta có đồ thị hàm số y = 2x
+ A(1;4)
=> xA = 1 ; yA = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2.1 ( vô lí )
=> A không thuộc đồ thị hàm số y = 2x
+ B = ( -1; -2 )
=> xB = -1 ; yB = -2
Thế vào đồ thị hàm số y = 2x ta có :
-2 = 2(-1) ( đúng )
=> B thuộc đồ thị hàm số y = 2x
+ C(-2; 4)
=> xC = -2 ; yC = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2(-2) ( vô lí )
=> C không thuộc đồ thị hàm số y = 2x
+ D(-2 ; -4 )
=> xD = -2 ; yD = -4
Thế vào đồ thị hàm số y = 2x ta có :
-4 = 2(-2) ( đúng )
=> D thuộc đồ thị hàm số y = 2x


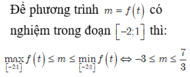

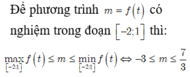
\(a^4+b^4+c^4\) ạ