1. Đường tròn ( C ) đi qua hai điểm A (4;3), B(-2;1) và có tâm nằm trên đường thẳng x +2y +5 =0. Viết phương trình đường tròn ( C).
2. Trong mặt phẳng Oxy, cho điểm M(3;-1) và đường thẳng (Δ): 2x - y + 3 =0. Hình chiếu H của điểm M trên đường thẳng (Δ) có tọa độ là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 5 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
28 tháng 5 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔANB và ΔACN có
góc ANB=góc ACN
góc NAB chung
=>ΔANB đồng dạng với ΔACN
=>AN^2=AB*AC
4 tháng 7 2023
a: góc ACB=1/2*sđ cung AB=90 độ
=>ΔACN vuông cân tại C
góc ACN+góc AMN=180 độ
=>AMNC nội tiếp
b: AMNC nội tiếp
=>góc CNA=góc CMA=góc BMD
góc BNE=1/2(sđ cung BE-sđ cung AC)
góc DMB=1/2*(sđ cung BD-sđ cung AC)
=>sđ cung BD=sđ cung BE
=>B nằm trên trung trực của DE
Xét ΔADB và ΔAEB có
góc ADB=góc aEB
AB chung
DB=BE
=>ΔABD=ΔAEB
=>AD=AE
=>A nằm trên trung trực của DE
=>AB là trung trực của DE
=>DE vuông góc AB
23 tháng 6 2019
a) Ta có đuờng tròn (I) tiếp xúc với AC tại A, theo tính chất góc tạo bởi tiếp tuyến và dây thì ^DAC = ^DBA
Tuơng tự ^DAB = ^DCA. Do đó ^BDC = ^DAB + ^DAC + ^DBA + ^DCA = 2(^DAB + ^DAC) = 2.^BAC = ^BOC
Suy ra 4 điểm B,D,O,C cùng thuộc một đuờng tròn theo quỹ tích cung chứa góc (đpcm).
b) Gọi đuờng thẳng AD cắt đường tròn đi qua 4 điểm B,O,D,C tại S khác D. Ta sẽ chỉ ra S cố định.
Thật vậy, gọi Dx là tia đối của tia DB. Ta có ^ODC = ^OBC = ^OCB = ^ODx => DO là phân giác ^CDx
Ta thấy hai đuờng tròn (O) và (I) cắt nhau tại A và B nên OI vuông góc AB
Mà AK vuông góc với AB (vì (K) tiếp xúc AB tại A) nên OI // AK. Tuơng tự OK // AI
Từ đây tứ giác AIOK là hình bình hành => IK chia đôi OA. Cũng dễ thấy IK là trung trực của AD
Theo đó IK chứa đuờng trung bình của \(\Delta\)AOD => IK // OD. Mà IK vuông góc AD nên OD vuông góc AD
Kết hợp với OD là phân giác của ^CDx => AD là phân giác của ^BDC (do ^CDx và ^BDC bù nhau)
Hay DS là phân giác của ^BDC. Lại có ^BDC là góc nội tiếp đuờng tròn đi qua B,D,O,C
=> S là điểm chính giữa (BC không chứa O của đuờng tròn (BOC)
Vì B,O,C cố định nên điểm chính giữa (BC không chứa O của (BOC) cố định => S cố định
Vậy AD luôn đi qua S cố định (đpcm).
22 tháng 6 2023
Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t
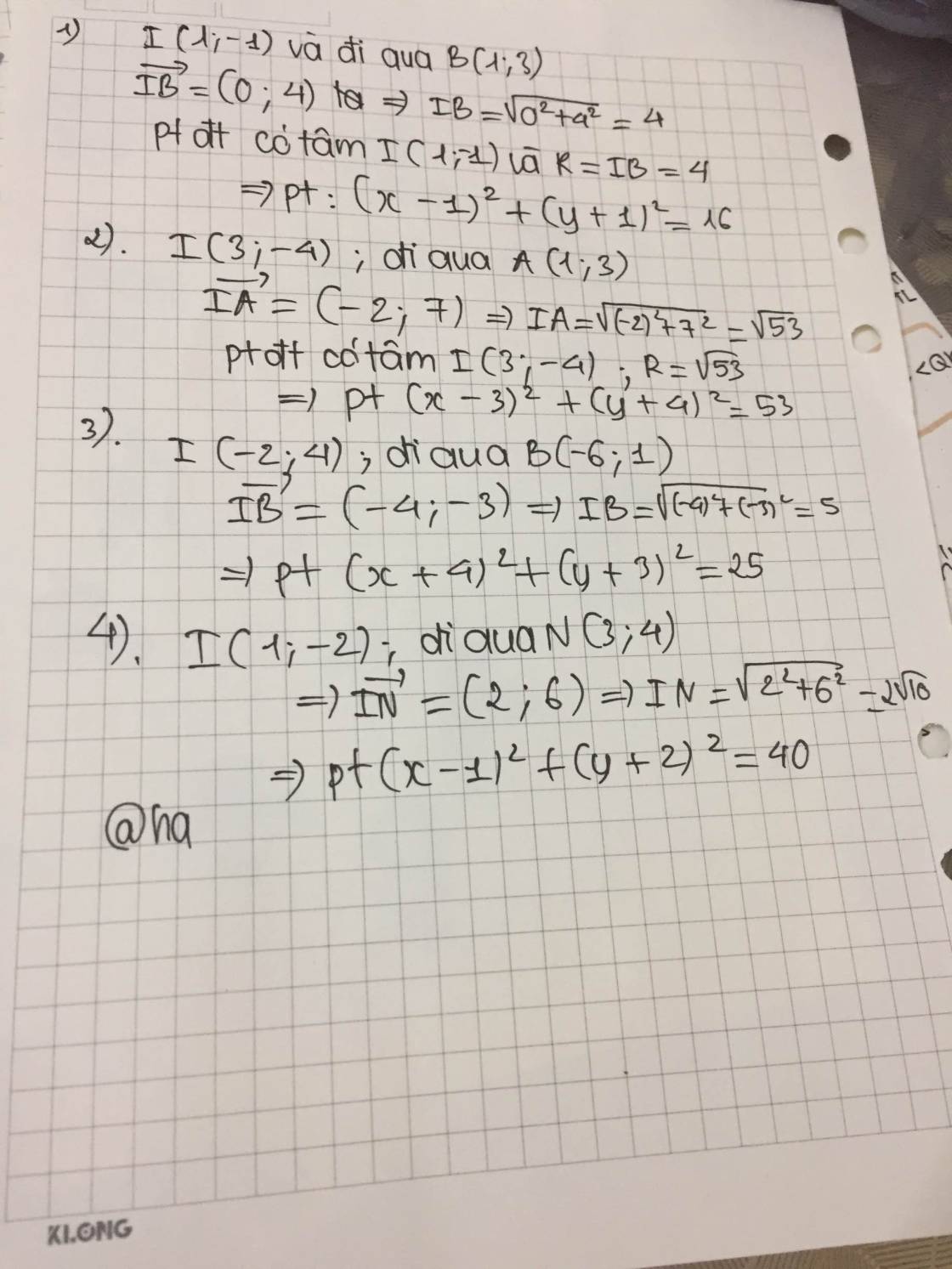
Làm sao để ra được I (-2t-5;t) vậy bạn
2)
Gọi (d) là đường thẳng qua M, H
Vì (d) vuông góc với (\(\Delta\)) => \(\overrightarrow{n_d}=\left(1;2\right)\)
có : (d) qua điểm M(3;-1) và 1 vtpt (1;2)
=> (d): \(\left(x-3\right)+2\left(y+1\right)=0\)
<=> (d) : \(x+2y-1=0\)
* \(H=\left(d\right)\cap\left(\Delta\right)\) nên tọa độ H là nghiệm của hệ:
\(\left\{{}\begin{matrix}2x-y+3=0\\x+2y-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Vậy tọa độ hình chiếu H(-1;1)