Cho △ABC cân tại A. Trung điểm cạnh BC là M(1;-2). Hình chiếu vuông góc của B xuống AC là N(3;-1). trung điểm cạnh AB thuộc ▲:x-2y=0. Tìm A,B
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét △ABM và △ACM có
AB=AC (theo giả thiết)
\(\widehat{B}\) = \(\widehat{C}\) (theo giả thiết)
MB=MC (theo giả thiết)
⇒△ABM=△ACM (c.g.c)
⇒\(\widehat{AMB}\) = \(\widehat{AMC}\) (hai góc tương ứng)
ABC

Bài 1 : a) M là trung điểm AB
N là trung điểm AC
suy ra : MN là Đường trung bình của tam giác ABC
suy ra : MN // BC ; MN = BC/2
b) Ta có : MN // BC và M là trung điểm AB
Mà AD cắt MN tại I nên từ đó suy ra : I là trung điểm của cạnh AD
em chỉ giải được bài 1 thôi nên thông cảm ạ


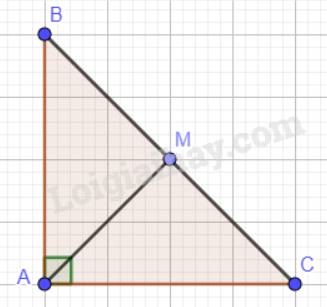
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).
Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).
Xét tam giác ABM và tam giác ACM có:
AB = AC
AM chung
BM = CM
\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)
\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)
\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).
Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).
Vậy tam giác MAB vuông cân tại M.

Vì tam giác ABC cân tại A suy ra AB=AC
Vì M là trung điểm BC suy ra BM=CM
Xét tam giác AMB và tam giác AMC có
AB=AC
cạnh AM chung
BM=CM
suy ra tam giác AMB =tam giác AMC (c.c.c)
suy ra góc AMC=góc AMB(hai góc tương ứng)
Mà góc AMC+góc AMB=180 độ
suy ra góc AMC bằng góc AMB=90 độ
suy ra AM vuông góc với BC
ghi cái định lí Pain vào vở đê
định lĩ six path or Pain : trong tam giác Cân đường trung tuyến ở đỉnh góc cân cắt cạnh đối diện tại 1 điểm bất kì thì suy ra nó vừa là trung tuyến Phân giác trung trực "

\(1,\left\{{}\begin{matrix}AM=MB\\AN=NC\end{matrix}\right.\Rightarrow MN\) là đtb \(\Delta ABC\Rightarrow MN=\dfrac{1}{2}BC.hay.2MN=BC\)
\(2,\) Vì \(MN//BC\left(t/c.đtb\right)\Rightarrow MNCB\) là hình thang
Mà \(\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân\right)\)
\(\Rightarrow MNCB\) là hthang cân
\(3,\left\{{}\begin{matrix}\widehat{MNO}=\widehat{OCB}\\\widehat{NMO}=\widehat{OBC}\end{matrix}\right.\Rightarrow\Delta MNO\sim\Delta COB\left(g.g\right)\\ \Rightarrow\dfrac{MN}{BC}=\dfrac{MO}{OC}\Rightarrow\dfrac{2MI}{2CK}=\dfrac{MO}{OC}\Rightarrow\dfrac{MI}{CK}=\dfrac{MO}{OC}\)
Lại có \(\widehat{IMO}=\widehat{OCK}\left(so.le.trong\right)\)
\(\Rightarrow\Delta IMO\sim\Delta KCO\left(c.g.c\right)\)
Do đó \(\widehat{MOI}=\widehat{KOC}\Rightarrow I;O;K\) thẳng hàng \(\left(1\right)\)
Chứng minh tương tự, ta được \(\Delta MAI\sim\Delta BAK\Rightarrow\widehat{AHE}=\widehat{BHF}\Rightarrow A;I;K\) thẳng hàng \(\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow A;I;O;K\) thẳng hàng
1) Xét ΔABC cân tại A, có:
M là trung điểm của AB, N là trung điểm của AC
⇒ MN là đường trung bình ΔABC
⇒ MN = 1/2BC ⇒ BC = 2MN (ĐPCM)
2) Xét tứ giác MNCB, có:
MN // BC(MN là đường trung bình)
MB = NC (do AB = AC và M, N là trung điểm AB, AC)
⇒ MNCB là hình thang.
mà:
\(\widehat{MBC}=\widehat{NCB}\) (do ΔABC cân tại A)
⇒ MNCB là hình thang cân.
d. Xét ΔAMN, có:
\(\widehat{AMN}=\widehat{ANM}\) (đồng vị so với \(\widehat{ABC},\widehat{ACB}\))
⇒ ΔAMN cân tại A, mà AI ⊥ MN (do MN là cạnh đáy, I là trung điểm MN) ⇒ A,I thẳng hàng
Chứng minh tương tự cho tam giác ABC với BC là cạnh đáy có K là trung điểm, ta được A, I, K thẳng hàng (1)
Có ΔMON cân, do \(\widehat{ONM}=\widehat{OMN}\) vì \(\widehat{BMN}=\widehat{CNM}\) ⇒ OI thẳng hàng do I là trung điểm cạnh đáy MN của tam giác cân. (2)
Từ (1) và (2) ⇒ A, I, O, K thẳng hàng.

Lời giải:
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
$\Rightarrow \widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=180^0$ nên $\widehat{AMB}=\widehat{AMC}+90^0$
$\Rightarrow AM\perp BC$
Xét tam giác $ABM$ vuông tại $M$, áp dụng định lý Pitago:
$BM=\sqrt{AB^2-AM^2}=\sqrt{13^2-12^2}=5$
$BC=2BM=2.5=10$