Cho z1; z2 là hai nghiệm phức của phương trình z2 - 2z + 4 = 0. Tìm phần thực, phần ảo của số phức: 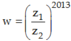 lần luợt là bao nhiêu, biết z1 có phần ảo dương.
lần luợt là bao nhiêu, biết z1 có phần ảo dương.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D
z ∈ R ⇔ z = z , ( z 1 + z 2 )= z 1 + z 2 , ( z 1 . z 2 )= z 1 . z 2

Đáp án: D.
z ∈ R ⇔ z = z , (z1 + z 2 ) = z 1 + z 2 , (z1. z 2 ) = z−1. z 2 .

Đặt z 1 = x 1 + i y 1 , z 2 = x 2 + i y 2 .
Từ giả thiết ta suy ra
x 1 2 + y 1 2 = x 2 2 + y 2 2 = 1 x 1 + x 2 2 + y 1 + y 2 2 = 3 ⇒ 2 x 1 y 1 + x 2 y 2 = 1
Suy ra:
z 1 - z 2 2 = x 1 - x 2 2 + y 1 - y 2 2 = x 1 - x 2 2 + y 1 - y 2 2 - 4 x 1 y 1 + x 2 y 2 = 3 - 2 = 1
Vậy z 1 - z 2 = 1
Đáp án D

Cách 1:
Gọi các số phức
z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i ( a 1 , b 1 , a 2 , b 2 ∈ ℝ )
z 1 - z 2 = a 1 - a 2 + b 1 - b 2 i z 1 + z 2 = a 1 + a 2 + b 1 + b 2 i
Ta có: z 1 = a 1 2 + b 1 2 = 3
⇒ a 1 2 + b 1 2 = 3
z 2 = a 2 2 + b 2 2 = 3 ⇒ a 2 2 + b 2 2 = 3
z 1 - z 2 = 2
⇔ a 1 - a 2 2 + b 1 - b 2 2 = 2 ⇔ a 1 - a 2 2 + b 1 - b 2 2 = 4 ⇔ a 1 2 + b 1 2 + a 2 2 + b 2 2 - 2 a 1 a 2 - 2 b 1 b 2 = 4 ⇔ 2 a 1 a 2 + 2 b 1 b 2 = 2
Do đó:
z 1 + z 2 = a 1 + a 2 2 + b 1 + b 2 2 = a 1 2 + b 1 2 + a 2 2 + b 2 2 + 2 a 1 a 2 + 2 b 1 b 2 = 8 = 2 2
Cách 2:
z 1 - z 2 2 = z 1 - z 2 z 1 ¯ - z 2 ¯ = z 1 2 + z 2 2 - z 1 z 2 ¯ + z 2 z 1 ¯ = 4 z 1 + z 2 2 = z 1 + z 2 z 1 ¯ + z 2 ¯ = z 1 2 + z 2 2 + z 1 z 2 ¯ + z 2 z 1 ¯ = 8 ⇒ z 1 + z 2 = 2 2
Cách 3:
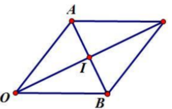
Gọi A, B lần lượt là điểm biểu diễn 2 số phức z 1 , z 2 . Khi đó tam giác OAB có O A = O B = 3 , A B = 2 . Gọi I là trung điểm của AB.
O I = O A 2 - A I 2 = 2 z 1 + z 2 = 2 O I ⇀ = 2 2
Chọn đáp án D.
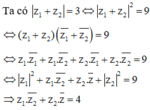


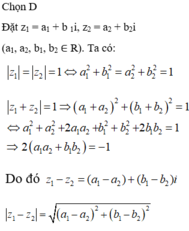
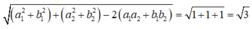
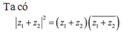
Chọn C.
Vì Δ = -3 nên phương trình có hai nghiệm phức: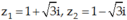 (do z1 có phần ảo dương)
(do z1 có phần ảo dương)
Ta có: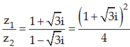
Do đó:
Vậy phần thực bằng 1, phần ảo bằng 0.