
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


z + 2 + i - z 1 + i = 0
z = - 2 + z + - 1 + z i
z = t > 0 ⇒ t = t - 2 2 + t - 1 2
⇔ t 2 - 6 t + 5 = 0 ⇔ t = 1 ; t = 5
Ta có t = 5 ( do t > 1 ) nên có
z = - 2 + z + - 1 + z i
= -2 + 5 + ( -1 + 5 )i = 3 + 4i
Đáp án cần chọn là D

Đáp án D
z + 2 + i − z ( 1 + i ) = 0 ⇔ ( a + b i ) + 2 + i − a 2 + b 2 ( 1 + i ) = 0 ⇔ a + 2 − a 2 + b 2 + ( b + 1 − a 2 + b 2 ) i = 0 ⇒ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇒ a − b + 1 = 0 ⇒ a = b − 1 ⇒ b + 1 − ( b − 1 ) 2 + b 2 = 0 ⇒ 2 b 2 − 2 b + 1 = b + 1 ⇒ b ≥ − 1 b 2 − 4 b = 0 ⇒ b = 0 b = 4 ⇒ a = − 1 ( L ) a = 3 ⇒ P = 4 + 3 = 7

Đáp án D.
Đặt
z = a + b i ⇒ a + b i + 2 + i − a 2 + b 2 1 + i = 0
⇔ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇔ a + 2 = b + 1 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 b 2 + 2 b + 1 = a 2 + b 2 ⇔ a = b − 1 b ≥ − 1 2 b + 1 = b − 1 2 ⇔ b = 0 ; a = − 1 b = 4 ; a = 3 .
Do z > 1 ⇒ a = 3 , b = 4.

Đáp án B.
Phương pháp:
Tọa độ hóa điểm số phức z, đánh giá GTNN.
Cách giải:
Giả sử z = x + y i , x , y ∈ R ⇒ M x ; y
là điểm biểu diễn của z trên mặt phẳng tọa độ Oxy.
P = 2 z + 1 + 2 z − 1 + z − z ¯ − 4 i
= 2 x + 1 2 + y 2 + x − 1 2 + y 2 + y − 2
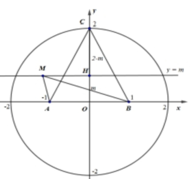
Đặt A − 1 ; 0 , B 1 ; 0 , C 0 ; 2 và H 0 ; y là hình chiếu của M lên Oy. Khi đó, P = 2 M A + M B + M C
Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, (M di chuyển trên hình tròn x 2 + y 2 ≤ 4 )
+) Nếu M ∈ C 1 : x 2 + y 2 ≤ 4 , y < 0 thì ta luôn tìm được điểm
M ' ∈ C 1 : x 2 + y 2 ≤ 4 , y ≥ 0 đối xứng với M qua Ox. Khi đó,
P = 2 M A + M B + H C
= 2 M ' A + M ' B + H ' C > 2 M A + M B + H C
+) Ta xét điểm
M ∈ C 2 : x 2 + y 2 ≤ 4 , y ≥ 0
Với M nằm trong nửa hình tròn C 2 , thay đổi trên đường thẳng y = m cố định 0 ≤ m ≤ 2 thì độ dài đoạn HC không đổi, M A + M B ≥ 2 2 H A + H C
Ta có:
2 H A + H C = 2 m 2 + 1 + 2 − m = f m , m ∈ 0 ; 2
f ' m = 2 m 2 + 1 − 1 , f ' m = 0 ⇔ m = 1 3
f m min = f 1 3 = 1 + 3 2
⇒ P min = 2 1 + 3 2 = 2 + 3
khi M 0 ; 1 3 hay z = i 3 .

Đáp án B.
Phương pháp:
Tọa độ hóa điểm số phức z, đánh giá GTNN.
Cách giải:
Giả sử z = x + y i , x , y ∈ R ⇒ M x ; y
là điểm biểu diễn của z trên mặt phẳng tọa độ Oxy.
P = 2 z + 1 + 2 z − 1 + z − z ¯ − 4 i
= 2 x + 1 2 + y 2 + x − 1 2 + y 2 + y − 2
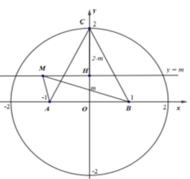
Đặt A − 1 ; 0 , B 1 ; 0 , C 0 ; 2 và H 0 ; y là hình chiếu của M lên Oy. Khi đó, P = 2 M A + M B + M C
Ta xác định vị trí của M để P đạt giá trị nhỏ nhất, (M di chuyển trên hình tròn x 2 + y 2 ≤ 4 )
+) Nếu M ∈ C 1 : x 2 + y 2 ≤ 4 , y < 0 thì ta luôn tìm được điểm
M ' ∈ C 1 : x 2 + y 2 ≤ 4 , y ≥ 0 đối xứng với M qua Ox. Khi đó,
P = 2 M A + M B + H C
= 2 M ' A + M ' B + H ' C > 2 M A + M B + H C
+) Ta xét điểm
M ∈ C 2 : x 2 + y 2 ≤ 4 , y ≥ 0
Với M nằm trong nửa hình tròn C 2 , thay đổi trên đường thẳng y = m cố định 0 ≤ m ≤ 2 thì độ dài đoạn HC không đổi, M A + M B ≥ 2 2 H A + H C
Ta có:
2 H A + H C = 2 m 2 + 1 + 2 − m = f m , m ∈ 0 ; 2
f ' m = 2 m 2 + 1 − 1 , f ' m = 0 ⇔ m = 1 3
f m min = f 1 3 = 1 + 3 2
⇒ P min = 2 1 + 3 2 = 2 + 3
khi M 0 ; 1 3 hay z = i 3 .
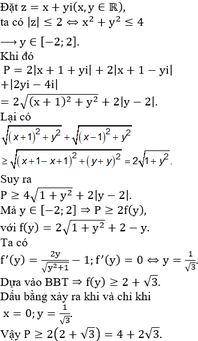

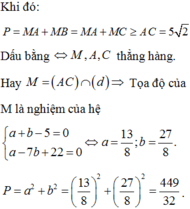

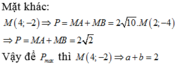

Chọn D