tam giác ABC cân tại A. Đường cao AH; trên tia đối của tia AH lấy D sao cho HD = HA. Trên tia đối của tia CB lấy E sao cho CE = CB
Chứng minh: a/ C là trọng tâm tam giác ADE
b/ AC cắt DE tại M. Chứng minh AE // HM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2022
Tham khảo
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
MA
29 tháng 5 2022
refer
a) Ta có: AB = AC (gt); AI = IB = 1/2AB (Cmt); AK = KC = 1/2 AC (gt)
AB = AI + IB
AC = AK + KC
=> AI = AK
Ta lại có: t/giác ABC cân tại A; AH là đường cao
=> AH là đường p/giác (t/c của t/giác cân)
=> góc BAH = góc CAH
hay góc IAG = góc KAG
b) Xét t/giác IAG và t/giác KAG
có IA = AK (cmt)
góc IAG = góc KAG (cmt)
AG : chung
=> t/giác IAG = t/giác KAG (c.g.c)
c) Ta có: AI = AK (cm câu b)
=> t/giác AIK cân tại A
=> góc AIK = góc AKI = (180 độ - góc A)/2 (1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = (180 độ - góc A)/2 (2)
Từ (1) và (2) suy ra góc AIK = góc B
Mà góc AIK và góc B ở vị trí đồng vị
=> IK // BC
17 tháng 12 2023
\(\dfrac{AI}{AH}=\dfrac{4}{5}\)
=>\(AI=\dfrac{4}{5}AH\)
Ta có: AI+HI=AH
=>\(HI=AH-AI=AH-\dfrac{4}{5}AH=\dfrac{1}{5}AH\)
\(\dfrac{AI}{IH}=\dfrac{\dfrac{4}{5}AH}{\dfrac{1}{5}AH}=\dfrac{4}{5}:\dfrac{1}{5}=4\)
Xét ΔBAH có BI là phân giác
nên \(\dfrac{BA}{BH}=\dfrac{AI}{IH}\)
=>\(\dfrac{10}{BH}=4\)
=>BH=10/4=2,5(cm)
ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
=>\(BC=2\cdot BH=5\left(cm\right)\)
Chu vi tam giác ABC là:
10+10+5=25(cm)
10 tháng 5 2023
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `\Delta ABH` và `\Delta ACH`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao của} \Delta ABC)$
`=> \Delta ABH = \Delta ACH (ch-gn)`
`b,`
Vì `\Delta ABH = \Delta ACH (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 cạnh tương ứng})$
`-> \text {AH là đường phân giác của}` `\Delta ABC`
`c,`
Vì `\Delta ABH = \Delta ACH (a)`
`-> \text {HB = HC}`
Ta có:
`\text {AH} \bot \text {BC}`
`\text {HB = HC}`
`-> \text {AH là đường trung trực của}` `\Delta ABC`.
MB
6
19 tháng 3 2016
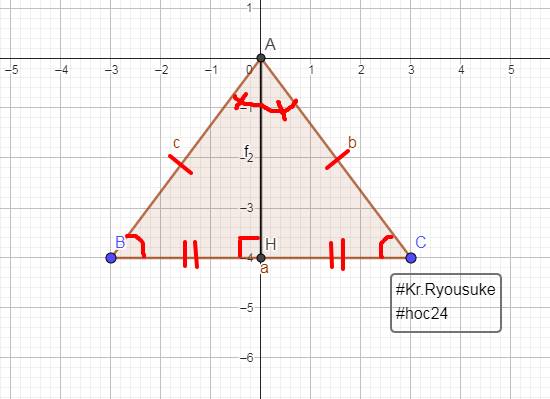
Ta có :
AC=AB=10cm (tg cân )
Tính: BC
Có : AC+AB=BC
=> 10+10=BC
=> 20 =BC
Chu vi hình tam giác ABC là :
10+10+20=40 cm
