Cho tam giác ABC. Trên tia đối tia BA, lấy D; trên tia đối AC lấy E sao cho CE = BD. CMR: DE > BC. Giúp mk với nha! Thanks các bạn nhìu!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
24 tháng 1 2024
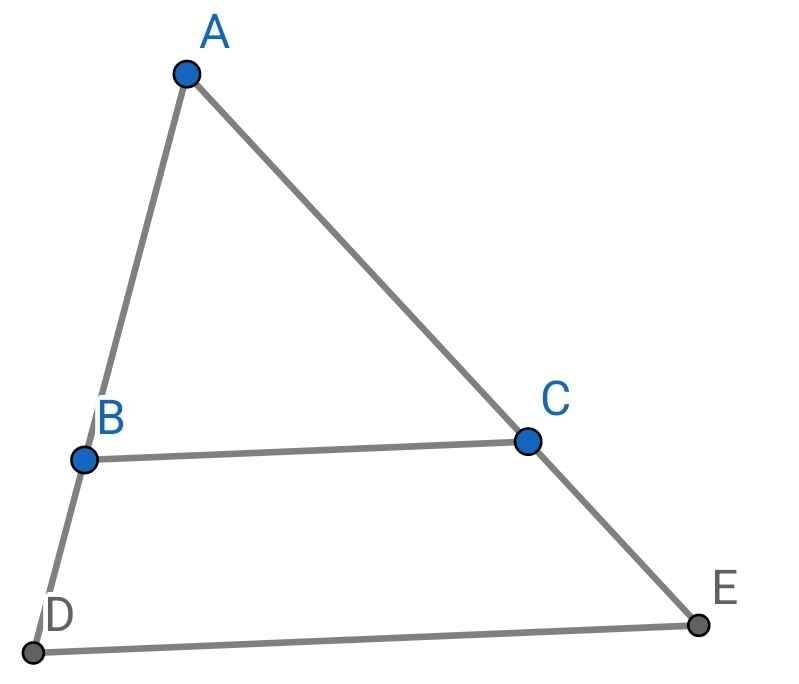Do 2BD = BA (gt)
⇒ AD = AB + BD
= 2BD + BD
= 3BD
⇒ AB/AD = 2/3 (1)
Do 2CE = CA (gt)
⇒ AE = AC + CE
= 2CE + CE
= 3CE
⇒ AC/AE = 2/3 (2)
Từ (1) và (2) ⇒ AB/AD = AC/AE = 2/3
Xét ∆ABC và ∆ADE có:
AB/AD = AC/AE (cmt)
A chung
⇒ ∆ABC ∽ ∆ADE (c-g-c)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 8 2023
A B C M D E N I
a/
Xét tg AMB và tg MNC có
MB=MC (giả thiết)
MA=MN (giả thiết)
\(\widehat{AMB}=\widehat{NMC}\) (góc đối đỉnh)
=> tg AMB = tg NMC (c.g.c)
b/ Nối A với I cắt BD tại M'
Xét tg ADE có
BE=BA (gt) => DE là trung tuyến của tg ADE
IE=ID (gt) => AI là trung tuyến của tg ADE
=> M' là trọng tâm của tg ADE => \(BM'=\dfrac{1}{3}BD\) (1)
Ta có
MB=MC (gt); MC=CD (gt) => MB=MC=CD
BD=MB+MC+CD
=> \(BM=\dfrac{1}{3}BD\) (2)
Từ (1) và (2) => \(M'\equiv M\)
=> A; M; I thẳng hàng
21 tháng 1 2021
a) Xét tg ABC và tg MBN có:
+ BA = BM (gt)
+ BC = BN (gt)
+ ^ABC = ^MBN ( 2 góc đối đỉnh)
Suy ra: tam giác ABC = tam giác MBN (c g c).
b) Xét tg NBC có: BN = BC (gt)
Suy ra: tg NBC cân tai B
Lại có: BO là đường trung tuyến ( do O là TĐ của NC)
Suy ra: BO cũng là đường cao (TC các đường trong tg cân)
Suy ra: BO vuông NC (đpcm)
c) Ta có: ^MNB + ^BNO = ^MNO
^ACB + ^BCO = ^ACO
Mà: ^MNB = ^ACB (do tg ABC = tg MBN)
^BNO = ^BCO (do tg NBC cân tại B)
Suy ra: ^MNO = ^ACO
Xét tg MNO và tg ACO:
+ ^MNO = ^ACO (cmt)
+ ON = OC (do O là Trung điểm của NC)
+ MN = AC (do tg ABC = tg MBN)
Suy ra: tg MNO = tg ACO (c g c)
Suy ra: OA = OM (2 cạnh tương ứng)
12 tháng 5 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
12 tháng 5 2023
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔACH
b: Xét tứ giác AHED có
B là trung điểm chung của AE và HD
=>AHED là hình bình hành
=>DE//AH
T
14 tháng 3 2020
GT:cho tam giác vuông ABC ( A vuông)
AC=AD ; DAC thẳng hàng;D khác C
KL: BA là tia phân giác của góc ABD
tam giác MBC=MBD
a), xét tam giác ABC và tam giác ADB có
AC=AD ( gt)
góc CAB=BAD ( đều = 90 độ )
AB cạnh cung
nên tam giác ABC = tam giác ADC (c-g-c)
mà Tam giác ACB = tam giác ADB
=>góc CBA = DBA ( 2 cạnh tương ứng)
mà ba nằm giữa
=> ba là tia phân giác của góc CBD
b), xét tam giác MBCvàMBD có
MB cạnh chung
Mặt Khác có góc CBA = DBA ( cm a)
mà góc CBA+ CBM=ABD+DBM
=> góc CBM=DBM
CB=BD (cm a)
nên tam giác MBC=MBD (c-g-c)
14 tháng 3 2020
a) Xét tam giác ABC và tam giác ADB có
AC=AD ( gt)
góc CAB=BAD ( đều = 90 độ )
AB cạnh chung
=> tam giác ABC = tam giác ADC (c-g-c)
Mà Tam giác ACB = tam giác ADB
=>góc CBA = DBA ( 2 cạnh tương ứng)
mà BA nằm giữa
=> BA là tia phân giác của góc CBD
b), xét tam giác MBC và MBD ,có :
MB cạnh chung
Mặt Khác có góc CBA = DBA ( cm a)
mà góc CBA+ CBM=ABD+DBM
=> góc CBM=DBM
CB=BD (cm a)
nên tam giác MBC=MBD (c-g-c)