Cho tam giác ABC có AB>AC.Lấy điểm D trên AB sao cho BD=CA, gọi E là trung điểm AD, gọi F là trung điểm của BC.CMR; góc BEF=1/2BAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 12 2018
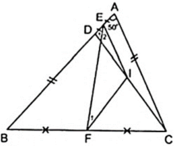
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác ACD và BCD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC
CM
17 tháng 5 2019
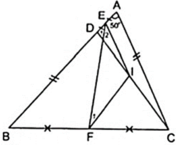
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.
Đặt BD = AC = 2a
Áp dụng định lý đường trung bình của hai tam giác trên ta có:
( 1 ) FI//BD ( 2 ) FI = a
( 3 ) EI = a ( 4 ) EI//AC
9 tháng 9 2017
Giải:
HÌNH TỰ VẼ
Qua \(I\) và \(D\), kẻ IN song song với \(BC;DM\) song song với \(BC\) \(\left(M;N\in AC\right)\)
Do \(\Delta ABC\) cân nên \(\Delta AMD\) cân.
\(\Rightarrow AM=AD\Rightarrow AM=CE\) \(\left(1\right)\)
Mặt khác \(IN\) song song với \(BC\) nên \(IN\) song song với \(MD\).
Xét \(\Delta EMD\) có \(I\) là trung điểm của \(DE\), \(IN\) song song với \(MD\) nên \(N\) là trung điểm của \(ME\). \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) => \(N\) là trung điểm của \(AC\) .
Xét\(\Delta ACK\) có \(N\) là trung điểm của \(AC\). \(NI\) song song với \(CK\) nên \(I\) là trung điểm của \(AK\).\(\left(\text{đ}pcm\right)\)
9 tháng 9 2017
Tham khảo nha:
Giải:
Qua I và D , kẻ IN song song với BC, DM song song với BC (M,N thuộc AC).
Do △ABC△ABC cân nên △AMD△AMD cân => AM=AD => AM=CE (1)
Mặt khác IN song song với BC nên IN song song với MD.
Xét △EMD△EMD có I là trung điểm của DE , IN song song với MD nên N là trung điểm của ME. (2)
Từ (1) và (2) => N là trung điểm của AC .
Xét △ACK△ACK có N là trung điểm của AC. NI song song vs CK nên I là trung điểm của AK.
(dpcm)
23 tháng 1 2022
a) Xét tam giác ABD: AB = AD (gt).
=> Tam giác ABD cân tại A.
Mà AH là phân giác góc BAD (gt).
=> AH là trung tuyến (Tính chất tam giác cân).
=> H là trung điểm của cạnh BD (đpcm).
23 tháng 1 2022
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
23 tháng 1 2022
a: Ta có: ΔABD cân tại A
mà AH là đường phân giác
nên H là trung điểm của BD
b: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
Suy ra: FB=FD
Xét ΔBFE và ΔDFC có
FB=FD
\(\widehat{FBE}=\widehat{FDC}\)
BE=DC
Do đó: ΔBFE=ΔDFC
Suy ra: \(\widehat{BFE}=\widehat{DFC}\)
mà \(\widehat{DFC}+\widehat{DFB}=180^0\)
nên \(\widehat{BFE}+\widehat{BFD}=180^0\)
=>D,E,F thẳng hàng
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 2 2018
Em tham khảo tại đây nhé.
Câu hỏi của Phạm Bá Gia Nhất - Toán lớp 7 - Học toán với OnlineMath
6 tháng 8 2018
Nối C với D. Gọi I là trung điểm CD. Nối I với M và N.
Xét \(\Delta\)CAD: M là trung điểm AD; I là trung điểm CD => IM là đường trung bình của \(\Delta\)CAD
=> IM = AC/2 (1)
Tương tự: IN là đường trung bình của \(\Delta\)CBD => IN = DB/2 (2)
Từ (1) và (2) => IM =IN => \(\Delta\)MIN cân ở I => ^IMN = ^INM.
Lại có: IN là đường trung bình \(\Delta\)CBD => IN // BD hay IN // BM => ^INM = ^BMN (So le trg)
=> ^IMN = ^BMN = 1/2 ^BMI.
Mặt khác: IM là đường trung bình \(\Delta\)CAD => IM // AC => ^BMI = ^BAC (Đồng vị)
=> ^BMN = 1/2. ^BAC hay ^BAC = 2.^BMN (đpcm).
18 tháng 12 2014
Vì D lần lượt là trung điểm của BC và AE suy ra: BD=CD và AE=ED
Xét tam giác ABD vs ECD có :
BD=CD ( gt)
AE=ED (gt)
Góc ABD = góc EDC ( Đối đỉnh )
Suy ra : Tan giác ABD=tam giác ECD ( c .g.c )
suy ra : góc BDA =goc BCE ( 2 góc tương ứng ) mà 2 góc này ở vị trí so le trong
suy ra : AB// CE