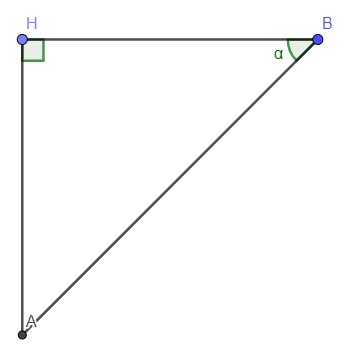
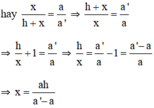Tính chiều cao của tháp ở bên kia sông biết BC = 50m; góc AHB= 32° và góc AHC= 46° và ba điểm B,C,H thẳng hàng ( kết quả làm tròn đến chữ số thập phân thứ nhất )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)

Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
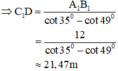
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.

Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)

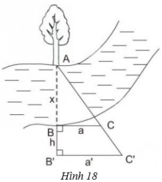
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 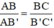 (hệ quả định lý Talet)
(hệ quả định lý Talet)