K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 10 2021
Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)
TM
21 tháng 7 2023
chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
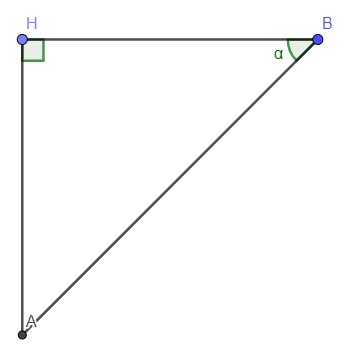
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)
9 tháng 12 2023
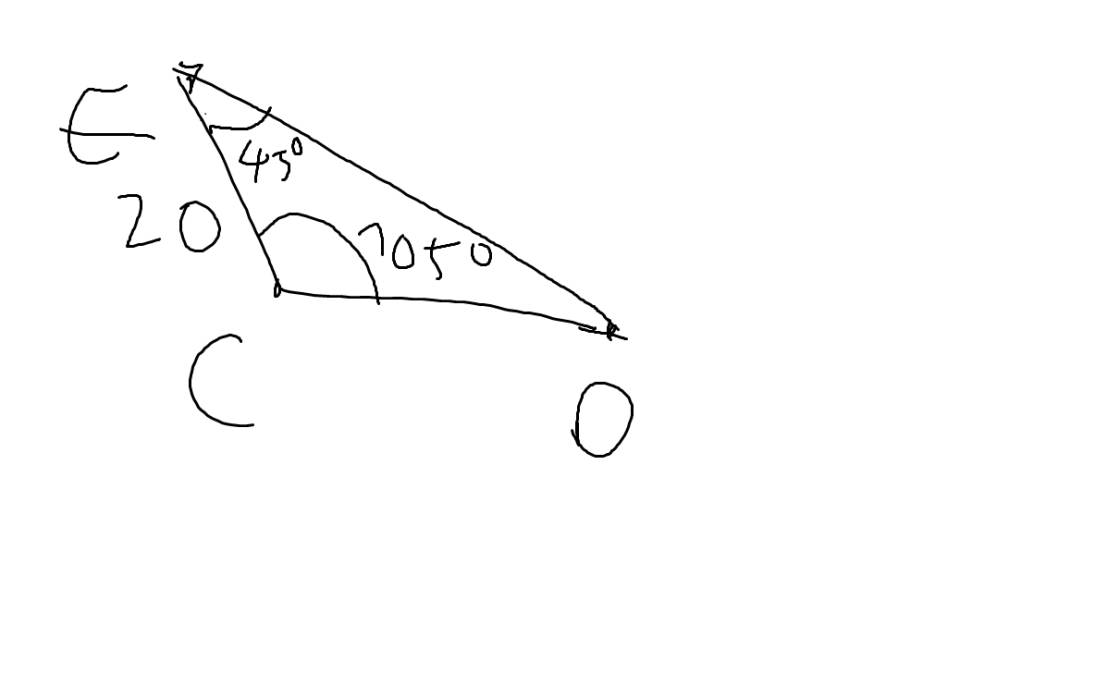
Xét ΔCED có \(\widehat{C}+\widehat{D}+\widehat{E}=180^0\)
=>\(\widehat{D}+105^0+45^0=180^0\)
=>\(\widehat{D}=30^0\)
Xét ΔCED có \(\dfrac{CE}{sinD}=\dfrac{CD}{sinE}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{sin30}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{\dfrac{1}{2}}=40\)
=>\(CD=40\cdot sin45=40\cdot\dfrac{\sqrt{2}}{2}=20\sqrt{2}\)
đề