Cho tam giác abc vuông tại a bm là phân giác của góc Vẽ mk vuông góc bc . Chứng minh rằng a) ba = bk ; b) bm là trung trực của đoạn ak ; c) Biết c = 40 độ . tính góc bmk ? ; d) Trên tia đối của tia ab lấy điểm i sao cho ai = ck . Chứng minh rằng ba điểm m ;i ; k thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2019
a) Xét \(\Delta BAM\)và \(\Delta BKM\) có:
\(\widehat{BAM}=\widehat{BKM}=90^o\left(gt\right)\)
BM là cạnh chung
\(\widehat{ABM}=\widehat{KBM}\)(BM là tia p/g của góc B)
\(\Rightarrow\Delta BAM=\Delta BKM\left(CH-GN\right)\)
\(\Rightarrow BA=BK\)(2 cạnh tương ứng)
b) Gọi H là giao điểm của BM và AK
Xét \(\Delta BAH\)và \(\Delta BKH\)có:
BA = BK (theo a)
\(\widehat{ABH}=\widehat{KBH}\)(BM là tia phân giác của góc B)
BH là cạnh chung
\(\Rightarrow\Delta BAH=\Delta BKH\left(c.g.c\right)\)
=> AH = KH (2 cạnh tương ứng) (1)
\(\widehat{BHA}=\widehat{BHK}\)(2 góc tương ứng)
Mà \(\widehat{BHA}+\widehat{BHK}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{BHA}=\widehat{BHK}=90^o\)
\(\Rightarrow BH\perp AK\)(2)
Từ (1) và (2) => BM là đường trung trực của AK
c) \(\Delta ABC:\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C=90^o}\)(trong tam giác vuông, 2 góc nhọn phụ nhau)
\(\Rightarrow\widehat{B}+40^o=90^o\)
\(\Rightarrow\widehat{B}=50^o\)
Vì BM là tia p/g của góc B
=> góc MBC=1/2 góc B= 1/2 . 50 độ = 25 độ
\(\Delta BMK:\widehat{BKM}=90^o\)
\(\Rightarrow\widehat{BMK}+\widehat{MBK}=90^o\)(trong tam giác vuông, 2 góc nhọn phụ nhau)
\(\Rightarrow\widehat{BMK}+25^o=90^o\)
\(\Rightarrow\widehat{BMK}=65^o\)
d) Tạm thời mk chưa nghĩ ra. Sorry bn nha!!!!
6 tháng 11 2017
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
15 tháng 3 2022
a: Xét ΔBAD vuông tại A và ΔBKD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)
Do đó: ΔBAD=ΔBKD
Suy ra: BA=BK
b: Ta có: ΔBAD=ΔBKD
nên DA=DK
mà DK<DC
nên DA<DC
CM
12 tháng 8 2019
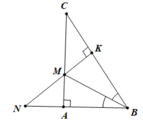
d. Trong tam giác ANC có hai đường cao CA và NK cắt nhau tại M nên M là trực tâm tam giác ANC (0.5 điểm)
Suy ra BM cũng là đường cao của tam giác ANC
BM vuông góc với CN (0.5 điểm)
2 tháng 3 2023
a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc HBA=góc HBE
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>KE vuông góc BC
19 tháng 5 2022
a: BC=5cm
b: XétΔBHK vuông tại H và ΔBAC vuông tại A có
BK=BC
góc HBK chung
Do đó: ΔBHK=ΔBAC
Suy ra: BH=BA
c: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
BA=BH
Do đó: ΔABE=ΔHBE
Suy ra: \(\widehat{ABE}=\widehat{HBE}\)
hay BE là phân giác của góc KBC
Ta có: ΔBKC cân tại B
mà BE là phân giác
nên BE là đường cao