Cho các số thực a,b sao cho tặp hợp { a2 + a ; b } và { b2 +b ; b } bằng nhau. Chứng minh rằng : a = b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì { a2 + a ; a } và { b2 + b ; b } bằng nhau nên ta có các trường hợp sau :
TH1 : a = b \( \implies\) a2 +a = b2 + b ( Luôn đúng )
TH2 : a2 + a = b và b2 + b = a
\( \implies\) a2 + a + b2 + b = a + b
\( \implies\) a2 + b2 = 0 ( 1 )
Ta có : a2 \(\geq\) 0 ; b2 \(\geq\) 0 \( \implies\) a2 + b2 \(\geq\) 0 ( 2 )
Từ ( 1 ) ; ( 2 ) Dấu " = " xảy ra \(\iff\) \(\hept{\begin{cases}a^2=0\\b^2=0\end{cases}}\) \(\iff\) \(\hept{\begin{cases}a=0\\b=0\end{cases}}\) \( \implies\) a = b = 0
KL : a = b

A = {0;1;2;3;4;5;6;7;8;9}
B = {0;2;4;6;8;10;...}
N* = {1;2;3;4;5;6;7;...}
\(A\subset N;B\subset N;N\cdot\subset N\)

a)\(A\subset N;B\subset N;N\cdot\subset N\)
b) A={0;1;2;3;...;9};B={1;3;5;7;...};N*={1;2;3;4;...}
c) A có 10 ptử, B và N* có vô số ptử

Chọn B
Cách giải: Ta có:
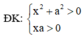
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
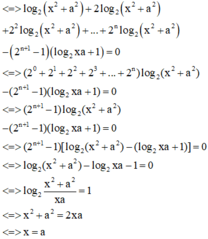
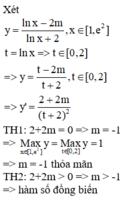
![]()
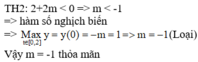

Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c khác 0
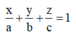
- Sử dụng bất đẳng thức
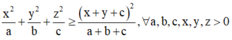
Đẳng thức xảy ra khi và chỉ khi
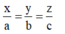
Cách giải:
![]()
Mặt phẳng (ABC) có phương trình:
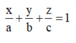
Khoảng cách từ O đến (ABC):
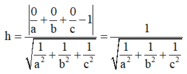
Ta có
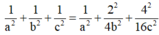
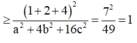
Dấu “=” xảy ra khi và chỉ khi:
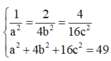
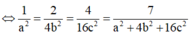
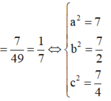
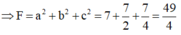

Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: 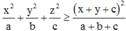
![]()
Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
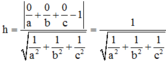
Ta có: 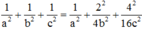
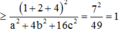
Dấu “=” xảy ra khi và chỉ khi:
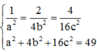
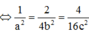
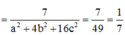
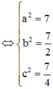
=> 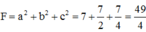

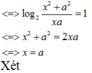
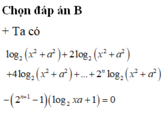


Đơn Giản thôi
Ta có \(\hept{\begin{cases}a^2+a=b\\b^2+b=b\end{cases}}\)Mà \(b=b\)nên \(a^2+a=b^2+b\)
Để \(a^2+a=b^2+b\)thì \(a^2=b^2\)và \(a=b\)(đpcm)
Vậy a=b
Nhật Khôi nè.Tau nghĩ là a2=b2 chưa chắc a=b. Nếu a và là hai số đối nhau thì bình lên cũng bằng nhau mà?