Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Có 
và tứ diện O.ABC vuông tại O nên:
Chọn đáp án B. Mẹo TN: Vì tính đối xứng cho
Chọn đáp án B.
Đáp án D.
Gọi D, K lần lượt là trung điểm của AB, OC. Từ D kẻ đường thẳng vuông góc với mặt phẳng (OAB). Và cắt mặt phẳng trung trực của OC tại I ⇒ I là tâm mặt cầu ngoại tiếp tứ diện OABC suy ra z 1 = c 2 .
Ta có S ∆ O A D = 1 2 . S ∆ O A B = 1 4 . a b = 1 2 . D E . O A ⇒ D E = b 2 .
Tương tự D F = a 2 ⇒ x 1 = a 2 , y = b 2 ⇒ I a 2 ; b 2 ; c 2 .
Suy ra x 1 + y 1 + z 1 = a + b + c 2 = 1 ⇒ I ∈ P : x + y + z - 1 = 0 .
Vậy khoảng cách từ điểm M dến (P) bằng d = 2015 3 .
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: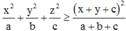
Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
Ta có: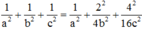
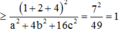
Dấu “=” xảy ra khi và chỉ khi:
=>