cho hình chóp S.ABCD; ABCD là hình vuông cạnh 2a; SA vuông góc với ABCD; SA = a căn 2. Kẻ AH vuôgn góc với Sb; AK vuông góc với SD. Chứng minh rằng: a) BC vuông góc SAB; b) BD vuông góc SAC; c) AH vuông góc SBC; d) SC vuông góc với AKH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C

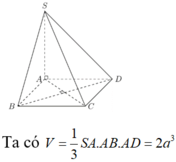
Áp dụng công thức thể tích của hình chóp ta có: V = 1 3 . h . S A B C D
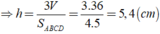
Chọn đáp án C.

Đáp án B
Dễ chứng minh
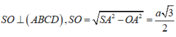
⇒ V c h o p = 1 3 S O . S A B C D = a 3 3 3

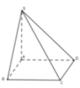
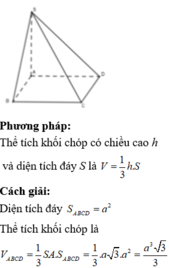
Diện tích đáy S A B C D = a 2
Thể tích khối chóp là
V A B C D = 1 3 S A . S A B C D = 1 3 . a 3 . a 2 = a 3 3 3
Chọn đáp án B.
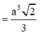

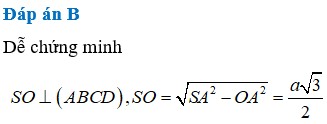


a: ta có: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
AB,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
b: Ta có: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
c: Ta có: BC\(\perp\)(SAB)
AH\(\subset\)(SAB)
Do đó: BC\(\perp\)AH
Ta có: AH\(\perp\)SB
AH\(\perp\)BC
SB,BC cùng thuộc mp(SBC)
Do đó: AH\(\perp\)(SBC)
d: Ta có: AH\(\perp\)(SBC)
SC\(\subset\)(SBC)
Do đó: AH\(\perp\)SC
Ta có: CD\(\perp\)SA(SA\(\perp\)(ABCD))
CD\(\perp\)AD(ABCD là hình vuông)
SA,AD cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
=>AK\(\perp\)CD
mà AK\(\perp\)SD
và CD,SD cùng thuộc mp(SCD)
nên AK\(\perp\)(SCD)
=>AK\(\perp\)SC
Ta có: SC\(\perp\)AK
SC\(\perp\)AH
AK,AH cùng thuộc mp(AKH)
Do đó: SC\(\perp\)(AKH)