Cho ba đường tròn (A; R1), (B; R2), và (C; R3) đôi một tiếp xúc noài nhau. Tính R1, R2, R3 biết AB=5cm, AC=6cm, BC=7cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (B) có
AC⊥AB tại A
nên AC là tiếp tuyến của (B;BA)
a: Xét (B) có AC⊥AB tại A
nên AC là tiếp tuyến của (B;BA)

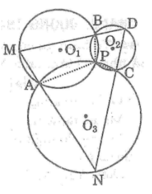
Gọi O1 , O2 ,O3 lần lượt là tâm của ba đường tròn
Ta có: ( O 1 ) cắt ( O 2 ) tại A, ( O 2 ) cắt ( O 3 ) tại C , ( O 3 ) cắt ( O 1 ) tại B
Suy ra: D là điểm nằm trên ( O 3 )
DB cắt ( O 1 ) tại M, DC cắt ( O 2 ) tại N
Nối MA, NA, PA, PB, PC ta có các tứ giác nội tiếp AMBP, BDCP và APCN
*Tứ giác APBM nội tiếp trong đường tròn ( O 1 ) nên ta có:


3/
a) theo tính chất 2 tiếp tuyến cắt nhau
ta có : DAB = BAH và HAC = CAE
DAH + HAE = 2(BAH + HAC) = 2.90 = 180
vậy D , A , E thẳng hàng
b,
b) gọi M là trung diểm của BC
mà DA = AE = R
⇒ MA là đường trung bình của hình thang BDEC nên MA // DB ⇒ MA ⊥ DE
mà MA = MB = MC nên MA là bán kính của đường tròn có đường kính BC
vậy DE là tiếp tuyến của đường tròn có đường kính BC
⇔ DE tiếp xúc với đường tròn có đường kính BC (đpcm)
bài 4 làm tương tự

a.
Gọi phương trình đường tròn (C) có dạng:
\(x^2+y^2-ax-by+c=0\)
Do A;B;C thuộc (C) nên: \(\left\{{}\begin{matrix}0+16-0.a-4b+c=0\\9+16-3a-4b+c=0\\9+0-3a-0.b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4b+c=-16\\-3a-4b+c=-25\\-3a+c=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=4\\c=0\end{matrix}\right.\)
Hay pt (C) có dạng: \(x^2+y^2-3x-4y=0\)
b.
Đường tròn (C) tiếp xúc (d) nên có bán kính \(R=d\left(C;d\right)=\dfrac{\left|3.3+0.4-5\right|}{\sqrt{3^2+4^2}}=\dfrac{4}{5}\)
Phương trình: \(\left(x-3\right)^2+y^2=\dfrac{16}{25}\)

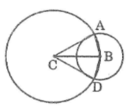
Xét hai tam giác ABC và DBC, ta có:
BA = BD (bán kính của (B; BA))
CA = CD (bán kính của (C; CA))
BC chung
Suy ra: ∆ ABC = ∆ DBC (c.c.c)
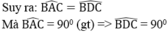
Suy ra: CD ⊥ BD tại D
Vậy CD là tiếp tuyến của đường tròn (B; BA)