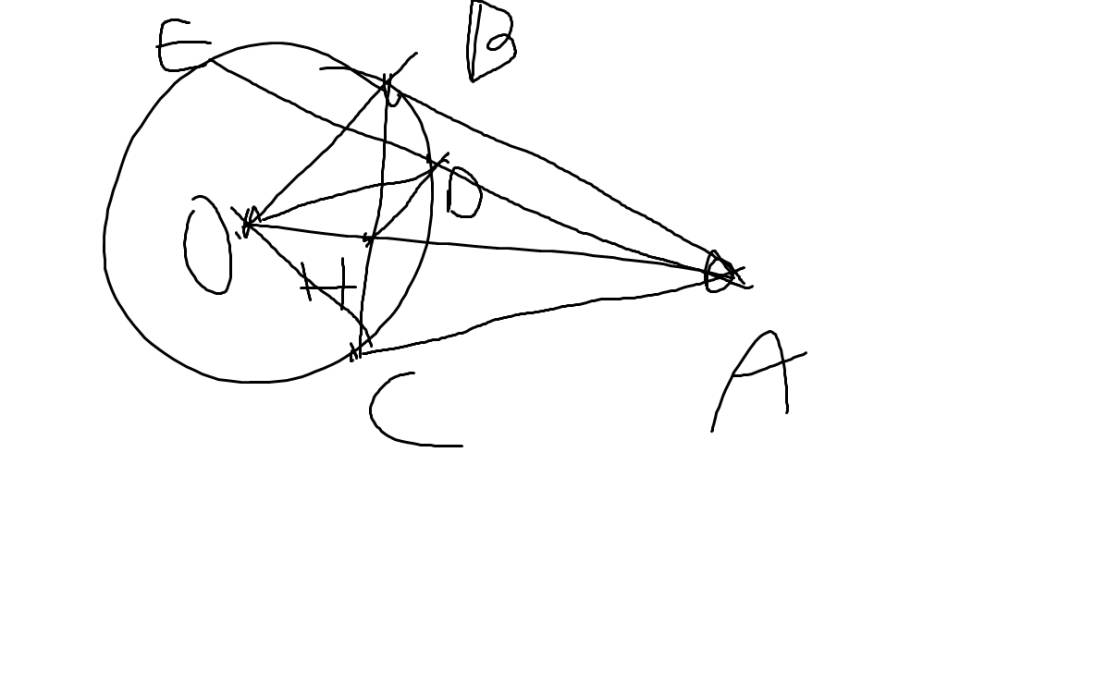
Từ điểm A ở ngoài (O; R) vẽ hai tiếp tuyến AB, AC( B, C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh OA vuông góc BC và OH.OA = R2
b) Vẽ đường kính BE của (O), AE cắt (O) tại D. Chứng minh ED.EA = 4OH.OA
c) Vẽ CI vuông góc với BE tại I, AE cắt CI tại K. Chứng minh HK // BE.


Mình chỉ biết làm câu a thôi nhé bạn 🙂🙂🙂.
a) Chứng minh OA vuông góc BC và OH.OA = R2
Xét (O) có:
✱ OB=OC (=R)
✱ AB=AC (tính chất 2 tiếp tuyến cắt nhau)
⇒ O,A thuộc đường trung trực của BC.
⇒ OA là đường trung trực của BC.
⇒ OA ⊥ BC tại đường trung điểm H của BC.
Xét ΔABO vuông tại B có đường cao BH (cmt) có:
OB2=OH.OA (hệ thức lượng) (1)
Mà OB=R (cmt) ⇒ OB2=R2 (2)
Từ (1) và (2) ⇒ OH.OA=R2