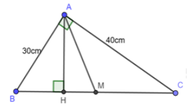
Cho tam giác ABC có = 90°, AB = 30cm, AC = 40cm, đường cao AH; BD là phân giác; I là giao điểm của AH và BD.
a) Chứng minh: Tam giác ABC đồng dạng với tam giác HAC
b) Tính AD và AH
c) Chứng minh AI=AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý Pytago cho ABH vuông tại A có:

Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
Vì AM là đường trung tuyến M là trung điểm BC
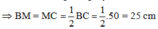
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A

Ta có
1 AH 2 = 1 AB 2 + 1 AC 2 ⇒ AH = 24cm tan B = A C A B = 40 30 ⇒ B ^ ≈ 53 0

BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!

a: Xét ΔABC vuông tại A và ΔEAC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEAC
BC=căn 30^2+40^2=50cm
AE=30*40/50=24cm
c: góc ADF=90 độ-góc ABD
góc AFD=góc BFE=90 độ-góc DBC
mà góc ABD=góc DBC
nên góc ADF=góc AFD
=>AD=AF

\(a.\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{B}chung.\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\)
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b.\) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=30^2+40^2=2500.\\ \Rightarrow BC=50\left(cm\right).\)
Xét \(\Delta ABC\) vuông tại A, đường cao AH:
\(AH.BC=AB.AC\) (Hệ thức lượng).
\(\Rightarrow AH.50=30.40.\\ \Rightarrow AH=24\left(cm\right).\)

a) Diện tích tam giác ABC là:
AB x AC : 2 = 40 x 30 : 2 = 600 (cm2)
b) Diện tích tam giác ABC là:
AH x BC : 2 = AH x 50 : 2 = AH x 25 = 600 (cm2)
=> AH = 600 : 25 = 24 (cm)
Đáp số: a) 600 (cm2)
b) 24 (cm)
tick mình nha
HT
a) Diện tích tam giác ABC là:
AB x AC : 2 = 40 x 30 : 2 = 600 (cm2)
b) Diện tích tam giác ABC là:
AH x BC : 2 = AH x 50 : 2 = AH x 25 = 600 (cm2)
=> AH = 600 : 25 = 24 (cm)
Đáp số: a) 600 (cm2)
b) 24 (cm)
tick cho mình để có động lực nha!
a: Xet ΔABC vuông tại A và ΔHAC vuông tại H có
goc C chung
=>ΔABC đồng dang với ΔHAC
b: \(BC=\sqrt{30^2+40^2}=50\left(cm\right)\)
AH=30*40/50=24(cm)
XétΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=40/8=5
=>AD=15cm
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AID=góc ADI
=>AI=AD
đúng kiến thức cô giáo mình dạy