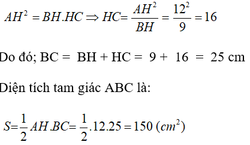Bài 12: Cho LA BC vuông tại A, đường cao AH . Cho BH = 9cm; H C =16 cm . a/ Tính độ dài AB, AC b/ HE LAB tại E,HF L AC tại F . Chứng minh: A E.A B = AF.A C c/ Lấy điểum K trên cạnh BC, kẻ KM I AB tại M, KN L AC tại N. Chứng minh tam giác HMN vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
18 tháng 10 2023
Đúng(0)
Những câu hỏi liên quan
H
Bài 3 : Cho tam giác ABC vuông tại A có đường cao AH. Biết AB = 9cm, BC = 25cm. Tính AB, AH, BH, CH.
1
16 tháng 9 2021
\(AC=\sqrt{BC^2-AB^2}=16\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=CH\cdot BH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=3,24\left(cm\right)\\HC=\dfrac{AC^2}{BC}=10,24\left(cm\right)\\AH=\sqrt{3,24\cdot10,24}=5,76\left(cm\right)\end{matrix}\right.\)
2 tháng 8 2021
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
NL
2
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
26 tháng 7 2021
Hình bạn tự vẽ nhé !
Xét tam giác ABC vuông tại A có đường cao AH
=> \(AB^2=BH.BC\) ( Hệ thức lượng trong tam giác vuông )
\(\Leftrightarrow BC=\frac{AB^2}{BH}=\frac{9^2}{5,4}=\frac{81}{5,4}=15\left(cm\right)\)
\(\Leftrightarrow CH=BC-BH=15-5,4=9,6\left(cm\right)\)
\(\Leftrightarrow AH^2=BH.CH\) ( Hệ thức lượng trong tam giác vuông )
\(\Leftrightarrow AH^2=5,4.9,6=51,84\Leftrightarrow AH=7,2\left(cm\right)\)
\(\Leftrightarrow AC^2=CH.BC\) ( Hệ thức lượng trong tam giác vuông )
\(\Leftrightarrow AC^2=15.9,6=144\Leftrightarrow AC=12\left(cm\right)\)
Đáp số : ...........
6 tháng 7 2022
$\begin{array}{l} {x^3} + a{x^2} + bx + c = \left( {x + 1} \right)P\left( x \right) + 2021\\ \Rightarrow P\left( { - 1} \right) = 2021 \Rightarrow - 1 + a - b + c = 2021\\ {x^3} + a{x^2} + bx + c = \left( {x - 2} \right)P\left( x \right) + 2030\\ \Rightarrow P\left( 2 \right) = 2030 \Rightarrow 8 + 4a + 2b + c = 2030 \end{array}$
$\begin{array}{l} \Rightarrow \left\{ \begin{array}{l} 4a + 2b + c = 2022\\ a - b + c = 2022 \end{array} \right. \Rightarrow 4a + 2b + c = a - b + c\\ \Rightarrow 3a + 3b = 0 \Leftrightarrow a = - b\\ \Rightarrow K = \left( {{a^{2021}} + {b^{2021}}} \right)\left( {{a^{2022}} + {b^{2022}}} \right) = \left( {{a^{2021}} - {a^{2021}}} \right)\left( {{a^{2022}} + {b^{2022}}} \right)\\ = 0\left( {{a^{2022}} + {b^{2022}}} \right) = 0 \end{array}$
b) Đặt $n^2-n+5=k^2(k\in \mathbb Z)$
$\begin{array}{l} \Rightarrow 4{n^2} - 4n + 20 = 4{k^2}\\ \Rightarrow {\left( {2n - 1} \right)^2} + 19 = {\left( {2k} \right)^2}\\ \Rightarrow \left( {2k - 2n + 1} \right)\left( {2k + 2n - 1} \right) = 19 \end{array}$
$\begin{array}{l} k \in \mathbb Z,n \in \mathbb Z \to 2k - 2n + 1,2k + 2n - 1 \in \mathbb Z\\ \bullet \left\{ \begin{array}{l} 2k - 2n + 1 = 1\\ 2k + 2n - 1 = 19 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} 2k = 2n\\ 2n + 2n = 20 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} k = \dfrac{{20}}{3}\\ n = \dfrac{{10}}{3} \end{array} \right.\left( L \right) \end{array}$
$\begin{array}{l} \bullet \left\{ \begin{array}{l} 2k - 2n + 1 = - 1\\ 2k + 2n - 1 = - 19 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 2k = 2n - 2\\ 2k + 2n = - 18 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} k = - 5\\ n = - 4 \end{array} \right.\left( {tm} \right)\\ \bullet \left\{ \begin{array}{l} 2k - 2n + 1 = 19\\ 2k + 2n - 1 = 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} k = 5\\ n = - 4 \end{array} \right.\left( {tm} \right)\\ \bullet \left\{ \begin{array}{l} 2k - 2n + 1 = - 19\\ 2k + 2n - 1 = - 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} k = - 5\\ n = 5 \end{array} \right.\left( {tm} \right) \end{array}$
Vậy $n=-4, n=5$ thỏa mãn yêu cầu bài toán.
T
1
8 tháng 9 2023
BC=BH+CH=13cm
Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC; AB^2=BH*BC; AC^2=CH*BC
=>\(AH=\sqrt{4\cdot9}=6\left(cm\right);AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right);AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\)
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
NT
0
CM
8 tháng 6 2017
Đáp án B
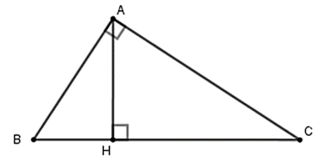
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
