Cho △ ABC vuông tại A , đường cao AH . Lấy d đối xứng với H qua AB , E đối xứng với qua AC . Chứng minh :
a) A ; D ; E thẳng hàng và A là trung điểm ED .
b) BD // CE .
c) BD + CE = BC .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

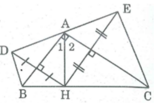
Điểm D đối xứng điểm H qua trục AB.
Suy ra AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực)
⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ∠ (DAH)
⇒ ∠ (DAB) = ∠ A 1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của góc (HAE) ⇒ ∠ A 2 = ∠ (EAC)
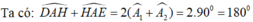
⇒ D, A, E thẳng hàng
Ta có: AD = AE (vì cùng bằng AH)
Suy ra điểm A là trung điểm của đoạn DE.
Vậy điểm D đối xứng với điểm E qua điểm A

a: Xét tứ giác AMHK có
góc AMH=góc AKH=góc KAM=90 độ
=>AMHK là hình chữ nhật
=>AH=MK
b: Xét ΔAHD có
AB vừa là đường cao, vừa là trung tuyến
nên ΔAHD cân tại A
=>AH=AD và AB là phân giác của góc HAD(1)
Xét ΔHEA có
AC vừa là đường cao, vừa là trung tuyến
nên ΔAHE cân tại A
=>AH=AE và AC là phân giác của góc HAE(2)
Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
c: Xét ΔAHB và ΔADB có
AH=AD
góc HAB=góc DAB
AB chung
=>ΔAHB=ΔADB
=>góc ADB=90 dộ
=>BD vuông góc DE(3)
Xét ΔAHC và ΔAEC có
AH=AE
góc HAC=góc EAC
AC chung
=>ΔAHC=ΔAEC
=>goc AEC=90 độ
=>CE vuông góc ED(4)
Từ (3), (4) suy ra BD//CE

a) Xét tứ giác AMHN có:
MÂN=AMH=ANH=90độ
=> AMHN là hình chữ nhật
b) Xét tam giác ANE và tam giác DME có
AN=DM(=MH)
NE=AM(=HN)
góc ANE = góc DMA (=90 độ)
Do đó tam giác ANE = tam giác DME (C-G-C)
=> góc ADM = NAE
Trong tam giác DMA vuông tại M có:
góc ADM +MAD=90
NAE + MAD=90
Ta có
DAE=DAM+MAN+NAE
DAE=90+DAM+NAE
DAE=90+90
DAE=180
Vậy D,A,E thẳng hàng

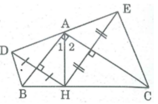
∆ ADB = ∆ AHB ⇒ BD = BH.
∆ AEC = ∆ AHC ⇒ CE = CH.
Vậy BD + CE = BH + CH = BC.

a: Ta có: H và D đối xứng nhau qua BA
nên AB là đường trung trực của HD
Suy ra: AB\(\perp\)HD và M là trung điểm của HD
Ta có: H và E đối xứng nhau qua AC
nên AC là đường trung trực của HE
Suy ra: AC\(\perp\)HE và N là trung điểm của HE
Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
Do đó: AMHN là hình chữ nhật

a: Xét tứ giác AKHM có
\(\widehat{AKH}=\widehat{AMH}=\widehat{MAK}=90^0\)
Do đó: AKHM là hình chữ nhật
Suy ra: AH=KM