cho hình bình hành ABCD (AB>CB). Hai đường chéo AC và DB cách nhau tại I. Từ A và C kẻ các đường thẳng vuông góc với AM ; CN xuống DB. Chứng minh rằng:
a) IM= IN
b) tứ giác AMCN là hình bình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì \(\left\{{}\begin{matrix}\widehat{AMD}=\widehat{BNC}=90^0\\AD=BC\\\widehat{ADM}=\widehat{CBN}\left(so.le.trong\right)\end{matrix}\right.\) nên \(\Delta AMD=\Delta CNB\left(ch-gn\right)\)
Do đó \(DM=BN\)
Mà I là giao 2 đg chéo hbh nên \(BI=ID\)
Vậy \(BI-BN=ID-DM\) hay \(IM=IN\)
b, Vì I là trung điểm AC và MN nên AMCN là hbh

b: Xét ΔADK vuông tại K và ΔCBH vuông tại H có
AD=CB
ˆADK=ˆCBHADK^=CBH^
Do đó: ΔADK=ΔCBH
Suy ra: DK=BH
Xét tứ giác BKDH có
DK//BH
DK=BH
Do đó: BKDH là hình bình hành

Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB(Hai cạnh đối của hình bình hành ABCD)
\(\widehat{D}=\widehat{B}\)(Hai góc đối của hình bình hành ABCD)
Do đó: ΔAED=ΔCFB(cạnh huyền-góc nhọn)
Suy ra: AE=CF(Hai cạnh tương ứng) và ED=FB(hai cạnh tương ứng)
Ta có: ED+EC=DC(E nằm giữa D và C)
FB+FA=AB(F nằm giữa A và B)
mà AB=DC(Hai cạnh đối của hình bình hành ABCD)
và ED=FB(cmt)
nên EC=FA
Xét tứ giác ECFA có
EC=FA(cmt)
EA=CF(cmt)
Do đó: ECFA là hình bình hành(Dấu hiệu nhận biết hình bình hành)

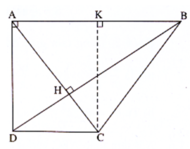
Hai đường chéo AC, BD cắt nhau tại H. Trong tam giác vuông ABD, ta có:
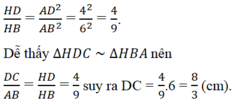
Kẻ đường cao CK của tam giác ABC, dễ thấy KB = AB – DC = 6 - 8/3 = 10/3.
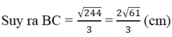
Tam giác vuông ABD có D B 2 = A B 2 + A D 2 = 6 2 + 4 2 = 52, từ đó DB = 52 = 2 13 (cm)

Ta có: BD⊥AB , DC⊥AC
Mà CH cũng ⊥ AB
=> CH//BD (1)
H là trực tâm ( giao điểm 2 hoặc 3 đường cao)
=> BH ⊥ AC
=> BH // DC (2)
Từ 1,2 => DBHC là hbh

b: Xét ΔDKO vuông tại K và ΔBHO vuông tại H có
OD=OB
\(\widehat{DOK}=\widehat{BOH}\)
Do đó: ΔDKO=ΔBHO
Suy ra: DK=BH
Xét tứ giác BKDH có
DK//BH
DK=BH
Do đó: BKDH là hình bình hành
a: Xét ΔAIM vuông tại M và ΔCIN vuông tại N có
IA=IC
\(\widehat{AIM}=\widehat{CIN}\)
Do đó: ΔAIM=ΔCIN
Suy ra: IM=IN