Cho hình thang ABCD vuông tại A và D, có AB = AD = 2; CD = 4. Độ dài \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=...\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LL
cho hình thang ABCD vuông tại A và D . Có AB=AD=\(\frac{DC}{2}\). Tính các góc B và C của hình thang
0
1 tháng 8 2023
a: BD=căn 15^2+20^2=25cm
OD=AD^2/BD=400/25=16cm
OB=25-16=9cm
AO=căn 16*9=12cm
ΔADC vuông tại D có DO là đường cao
nên AD^2=AO*AC
=>AC=20^2/12=400/12=100/3(cm)
b: DC=căn AC^2-AD^2=căn (100/3)^2-20^2=80/3cm
S ABCD=1/2*(AB+CD)*AD
=1/2*20*(15+100/3)=10*145/3=1450/3cm2
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2023
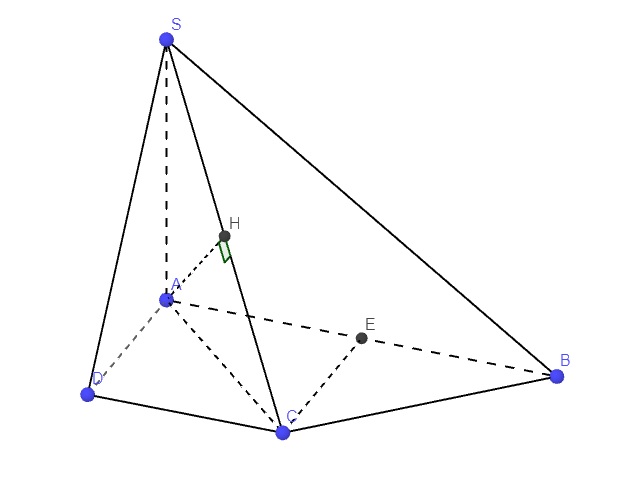
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)
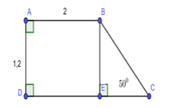
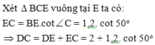
Đặt \(\overrightarrow{u}=\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{DC}=3.\overrightarrow{AB}+\overrightarrow{AD}\) (do \(\overrightarrow{DC}=2\overrightarrow{AB}\))
\(\Rightarrow\left|\overrightarrow{u}\right|^2=\left(3\overrightarrow{AB}+\overrightarrow{AD}\right)^2=9AB^2+AD^2+6\overrightarrow{AB}.\overrightarrow{AD}=9AB^2+AD^2=10AB^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=AB\sqrt{10}=2\sqrt{10}\)